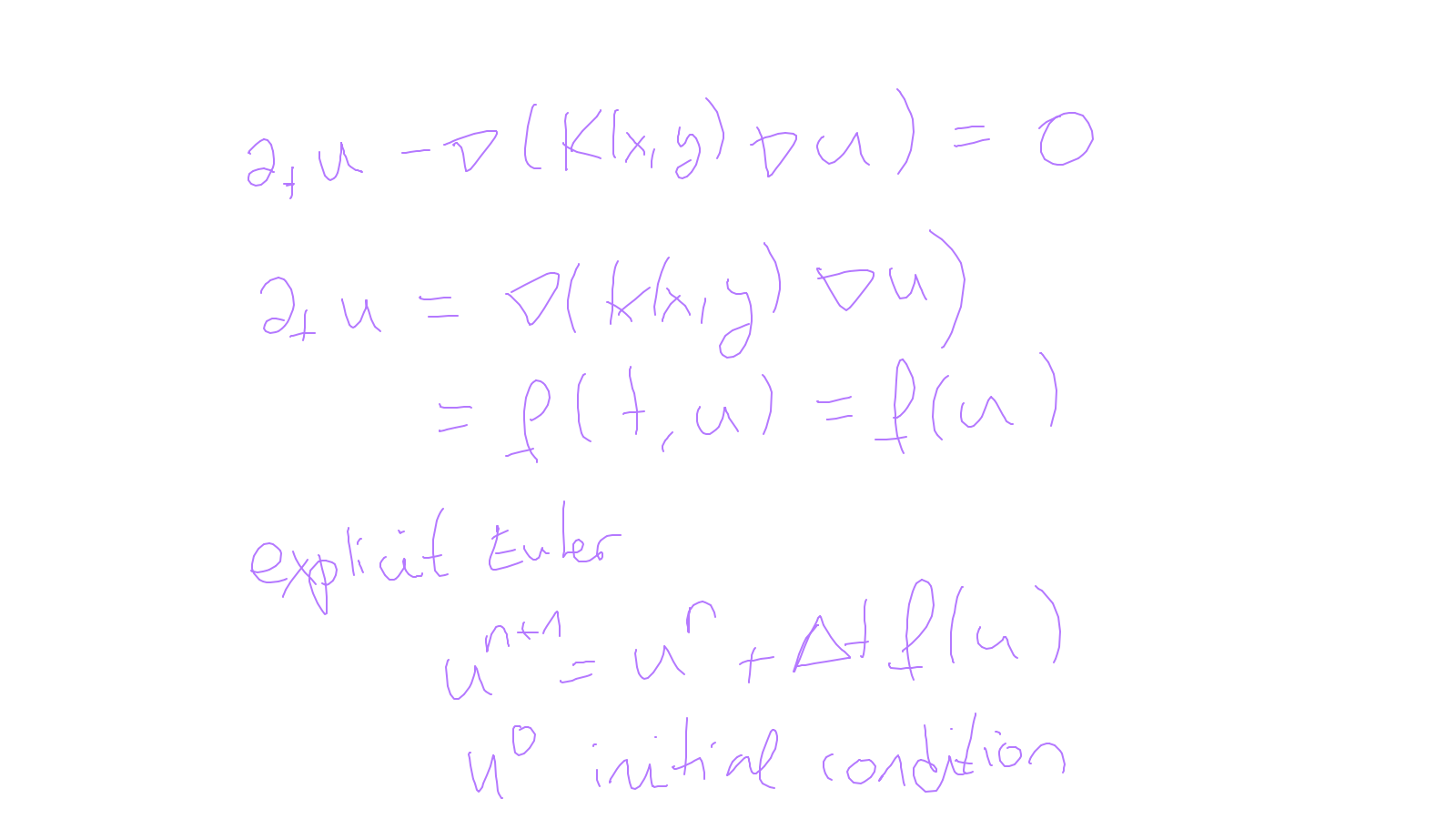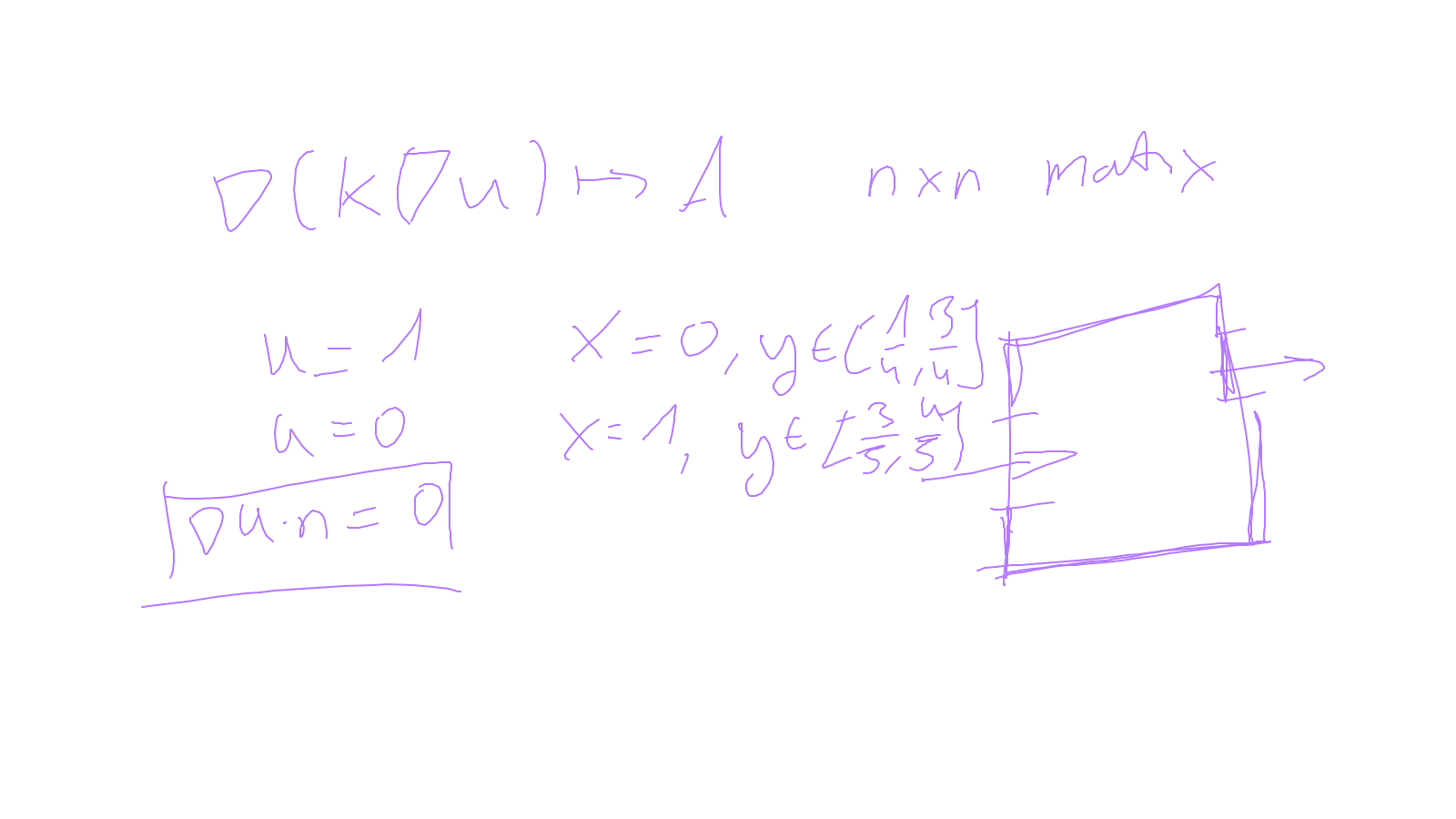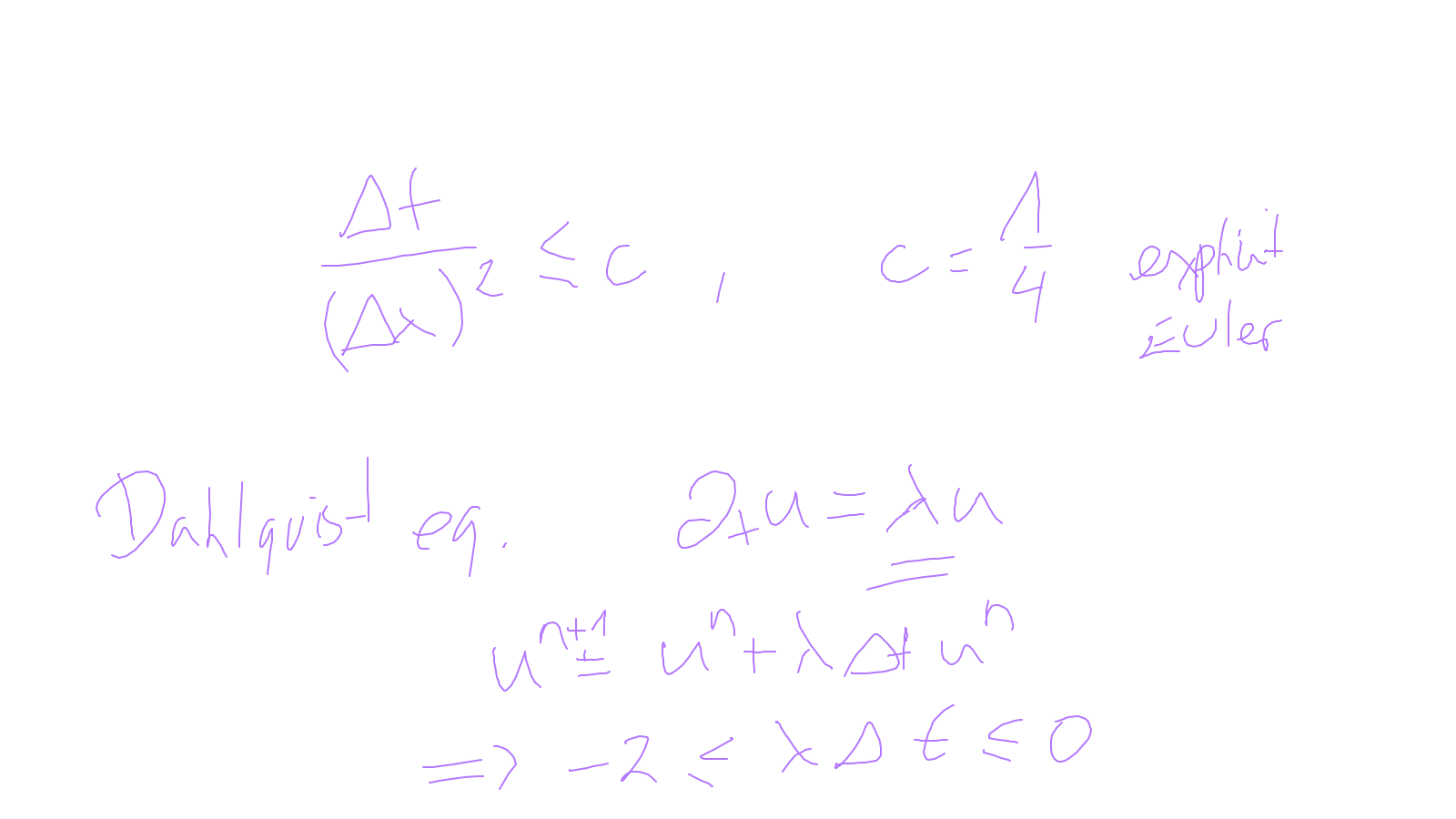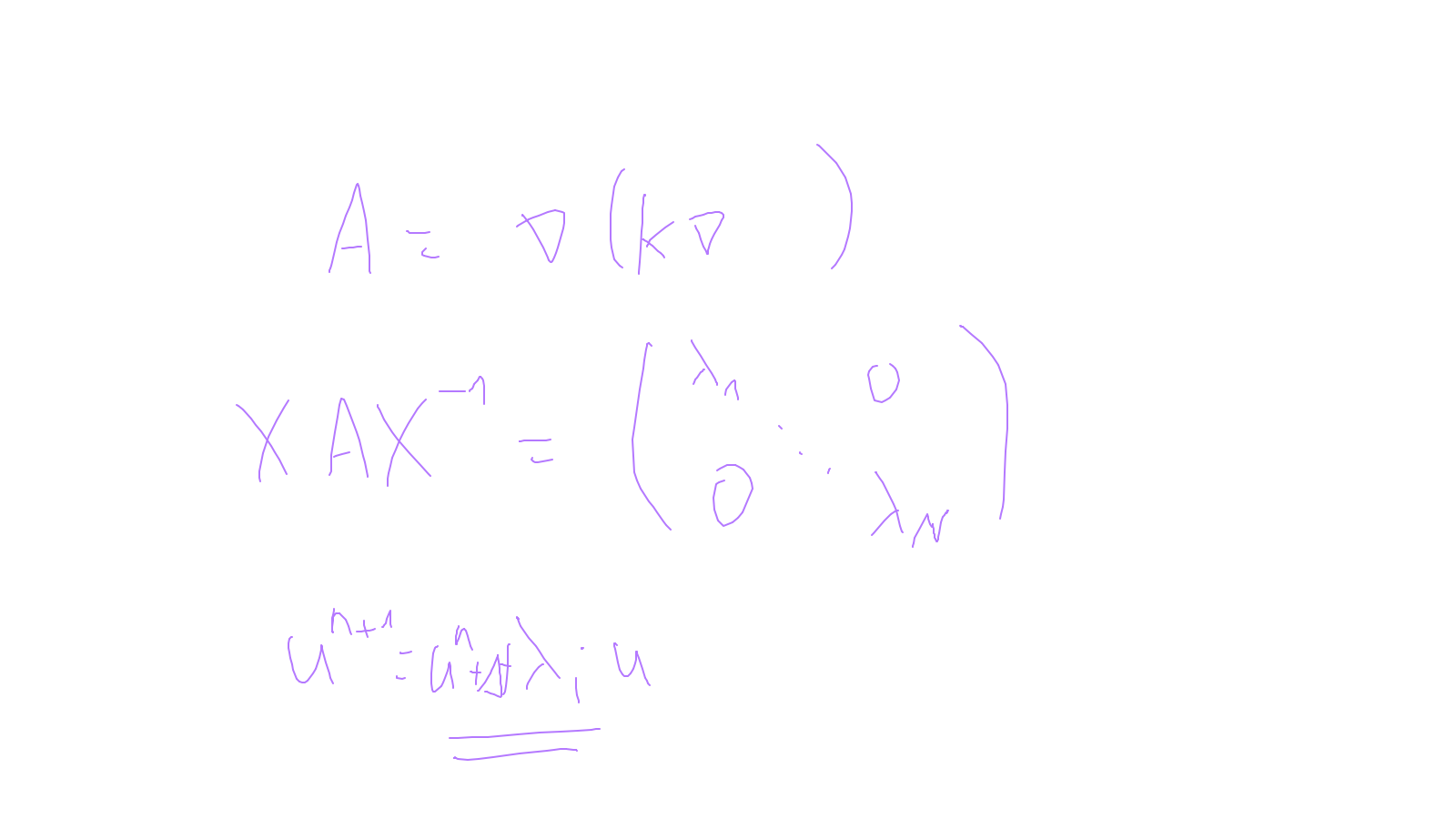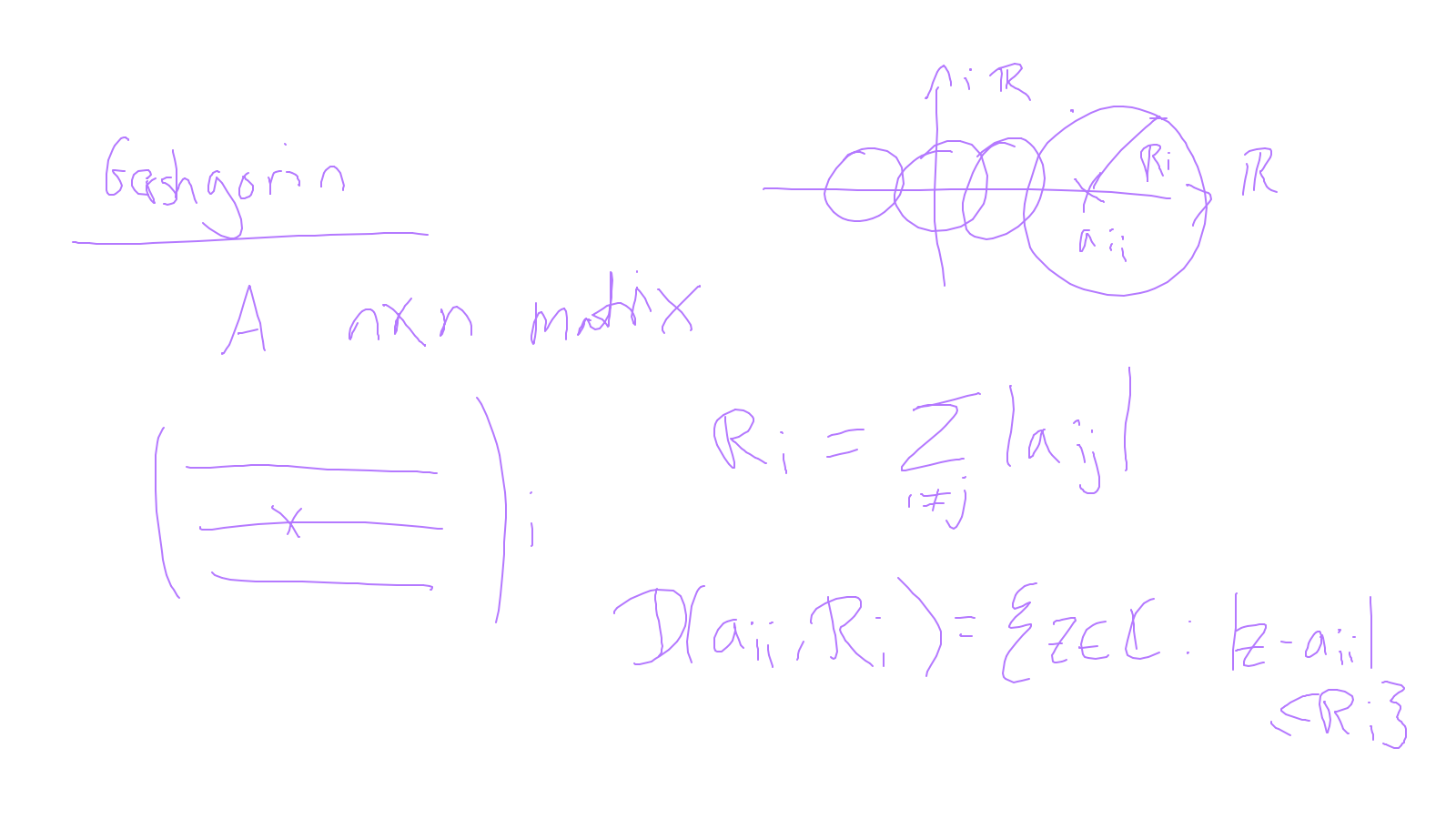Lecture 1: finite differences #
The lecture will take place over zoom. A calender invite is available on duo. The zoom invite can also be found at info).
Before the lecture it would be good if you can download the ipython notebook and run it. You can see jupyter for instructions on how to run the notebook.
Alternatively, you can run the notebook online without installing python.
After the lecture a video recording has been placed on duo. I apologise, the very end of the video has been cut off due to a technical issue. The video is now available at: video
The content of the whiteboard can be found below. It is also all contained in the ipython notebook itself.
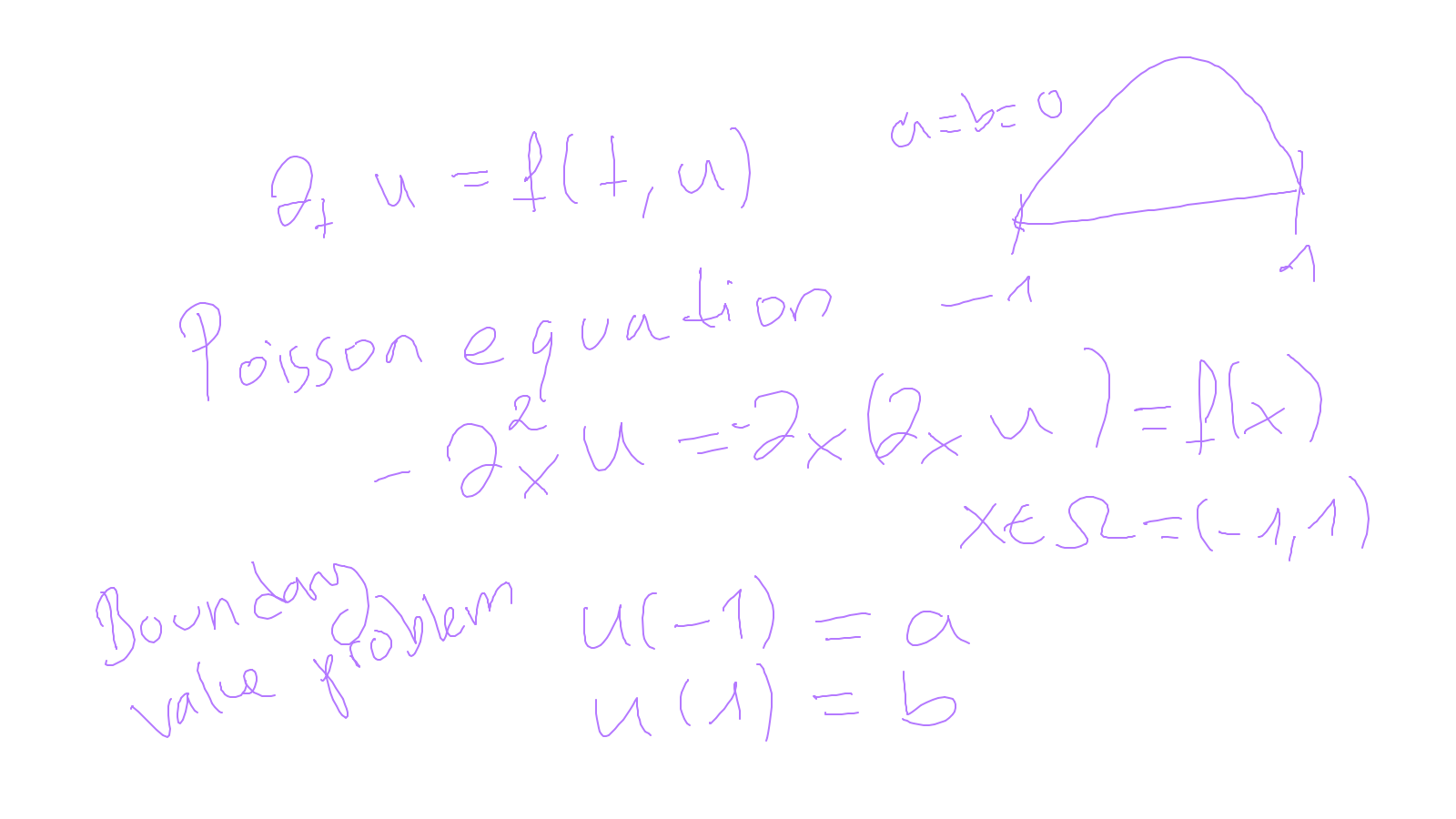

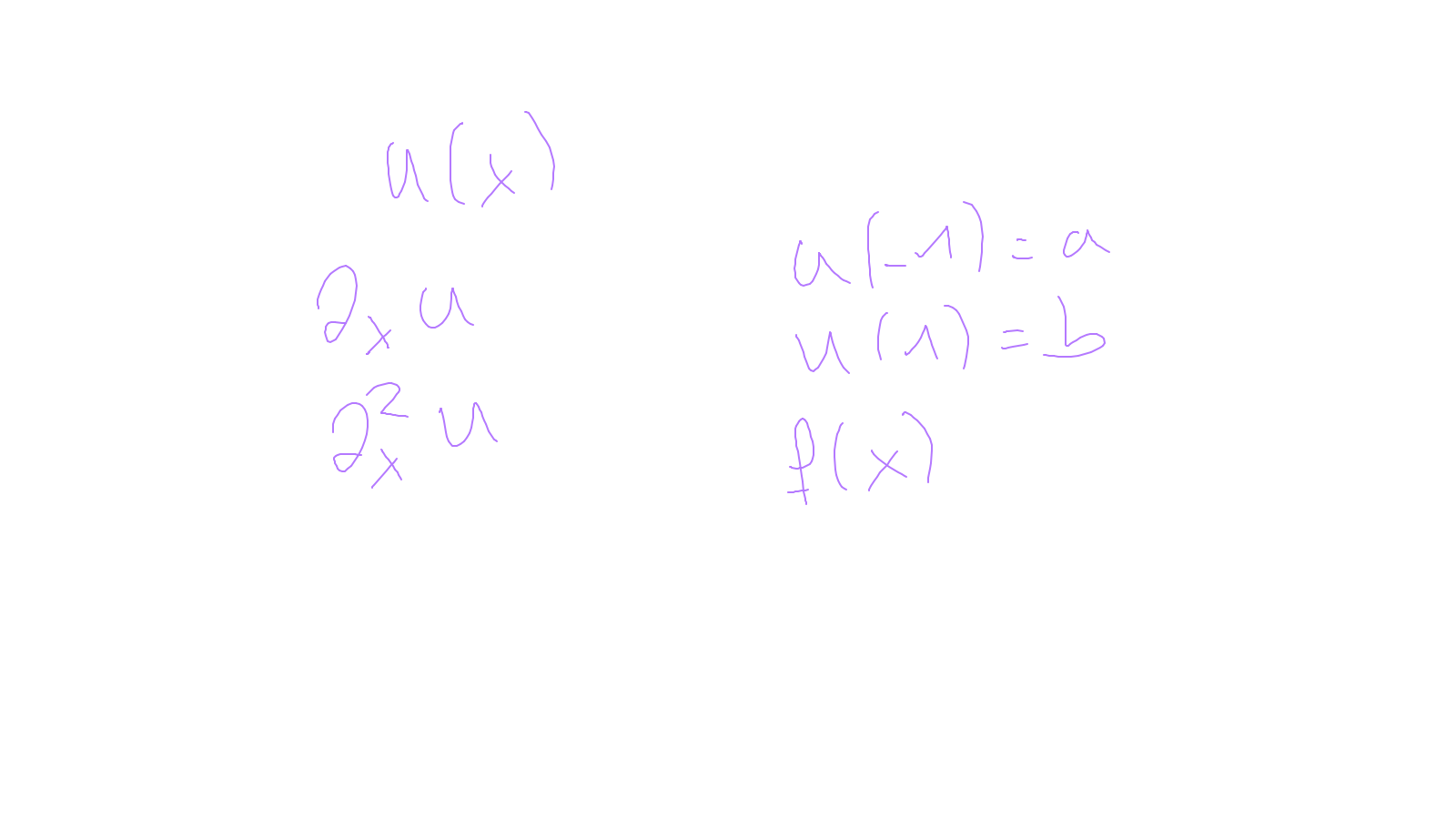
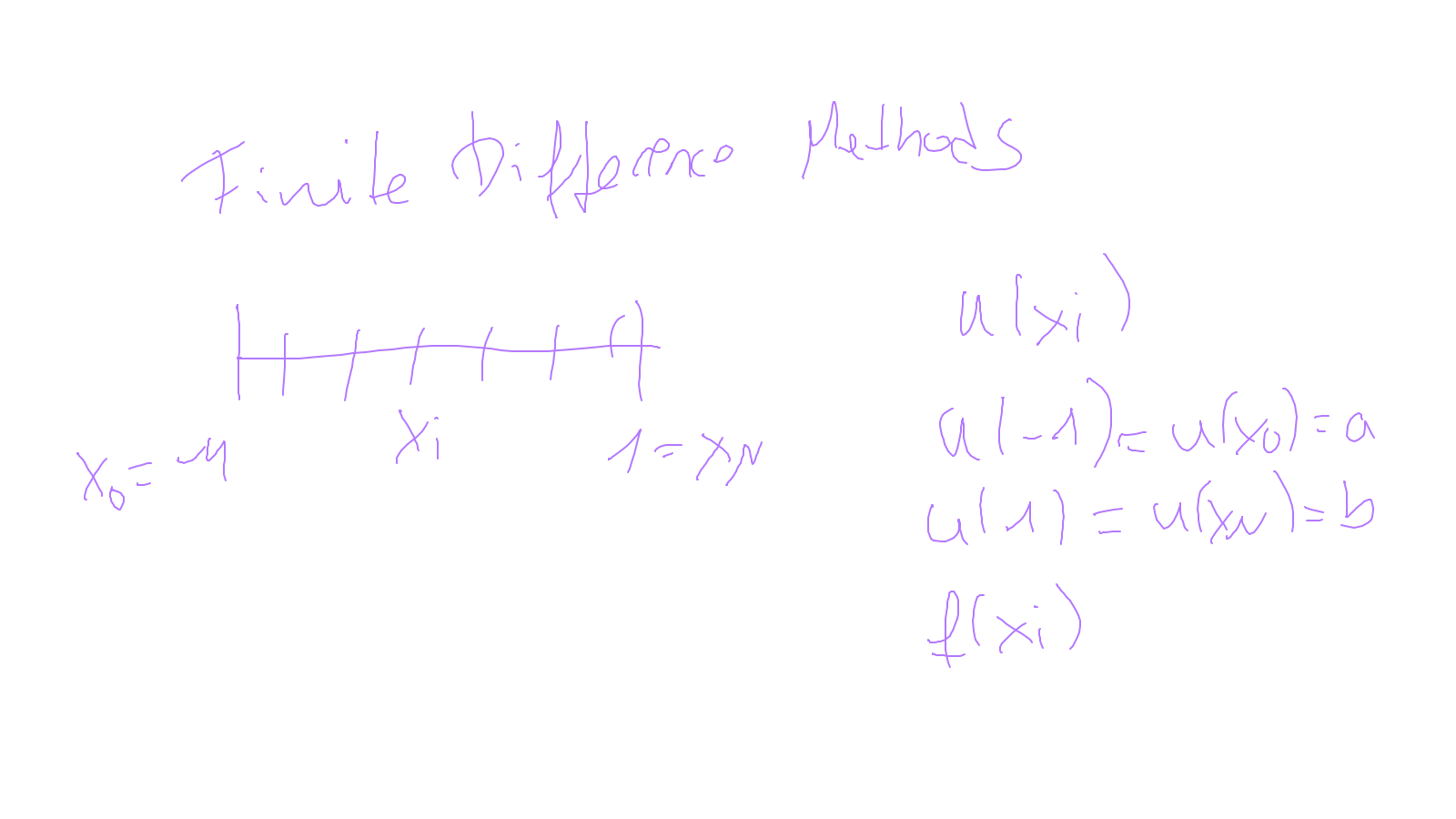
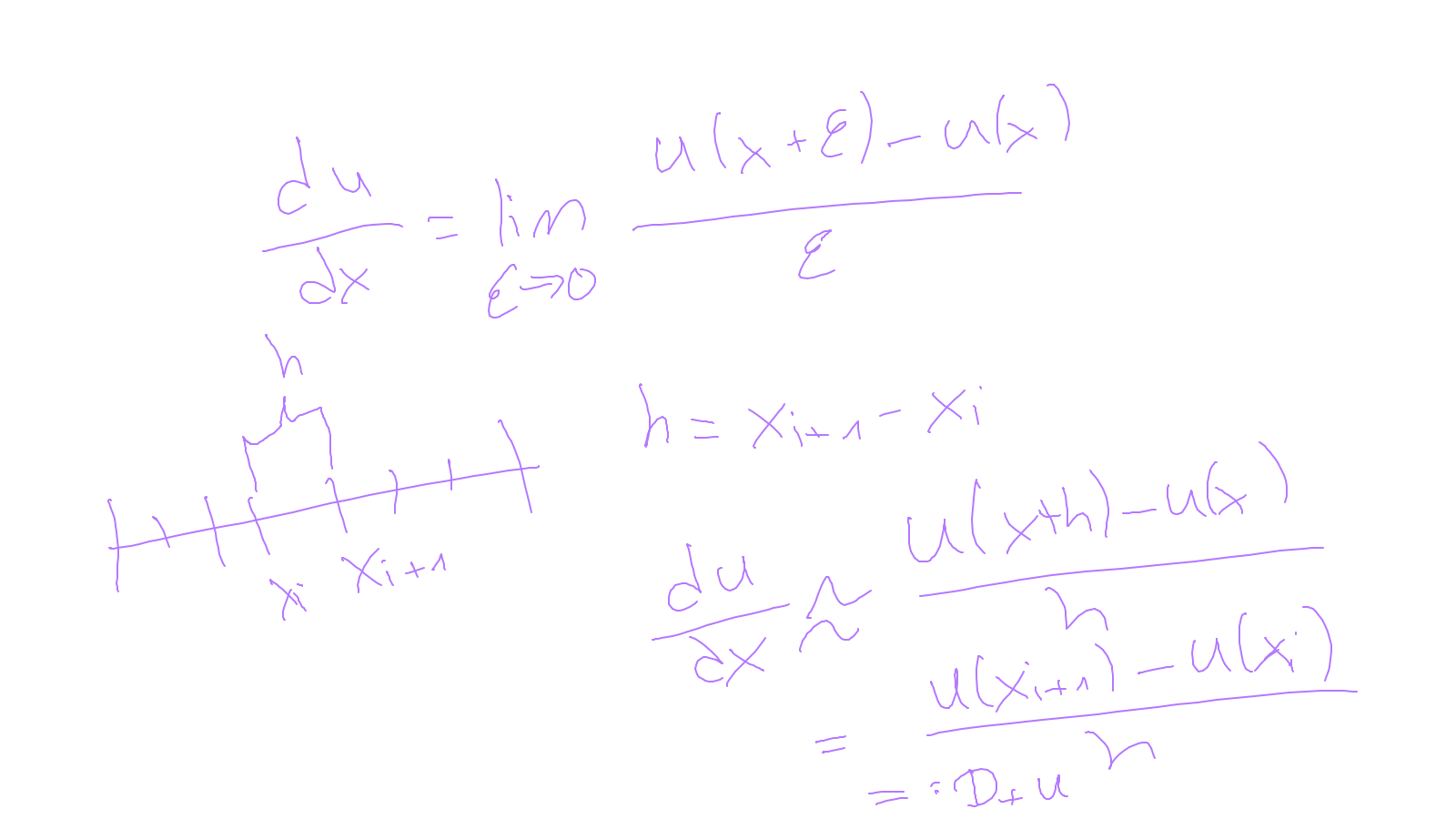
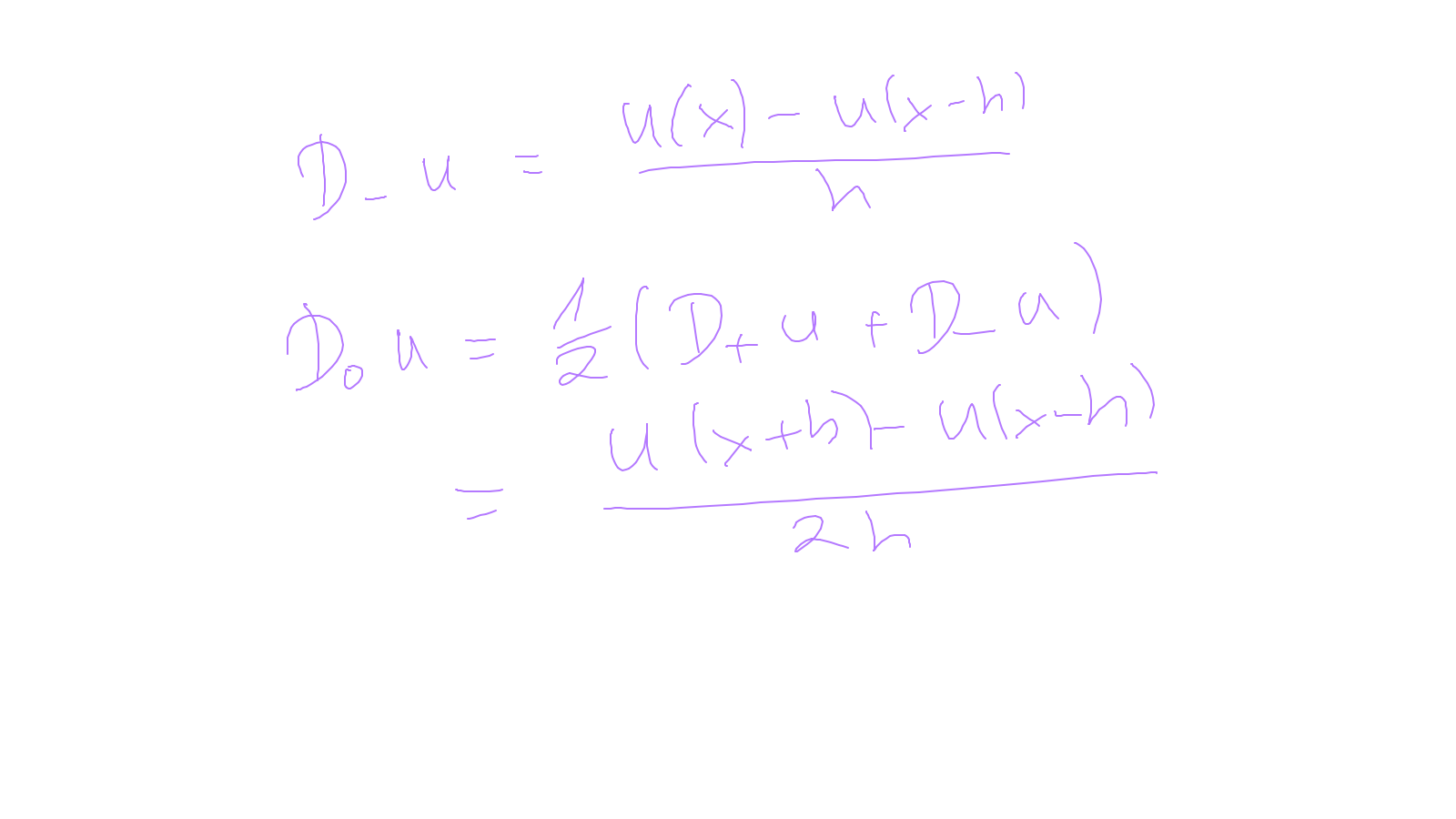
Lecture 2: finite differences #
For this lecture we continued with ipython notebook.
The notebook is also available online without installing python.
After the lecture a video recording has been placed on duo. The video is now available at: video
Lecture 3: finite differences #
We will be moving on to the next notebook during the next lecture. Before the lecture it would be good if you can download the next ipython notebook and run it. You can see jupyter for instructions on how to run the notebook.
Alternatively, you can run the notebook online without installing python.
The video is now available at: video
The content of the whiteboard can be found below. It is also all contained in the ipython notebook itself.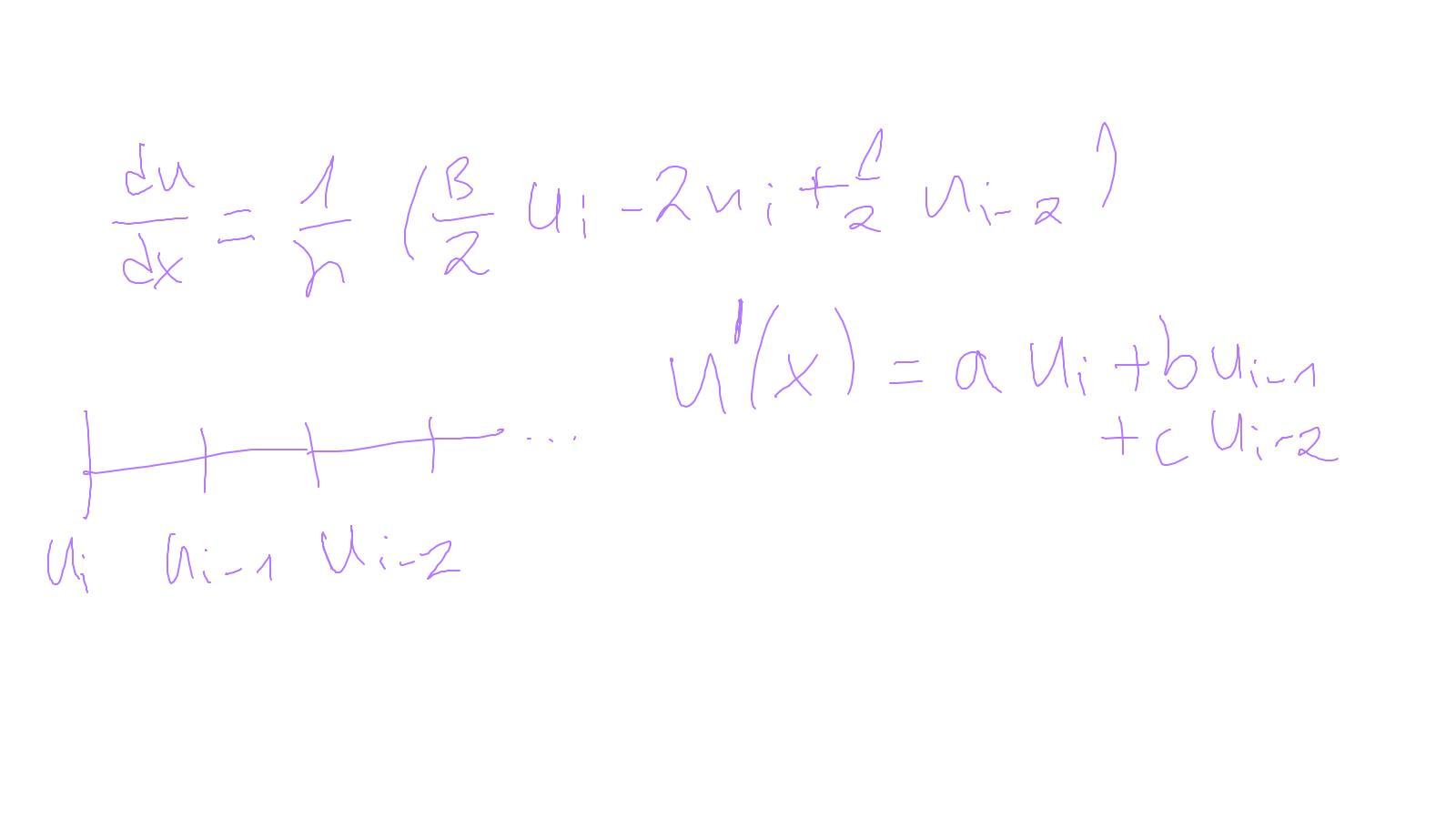
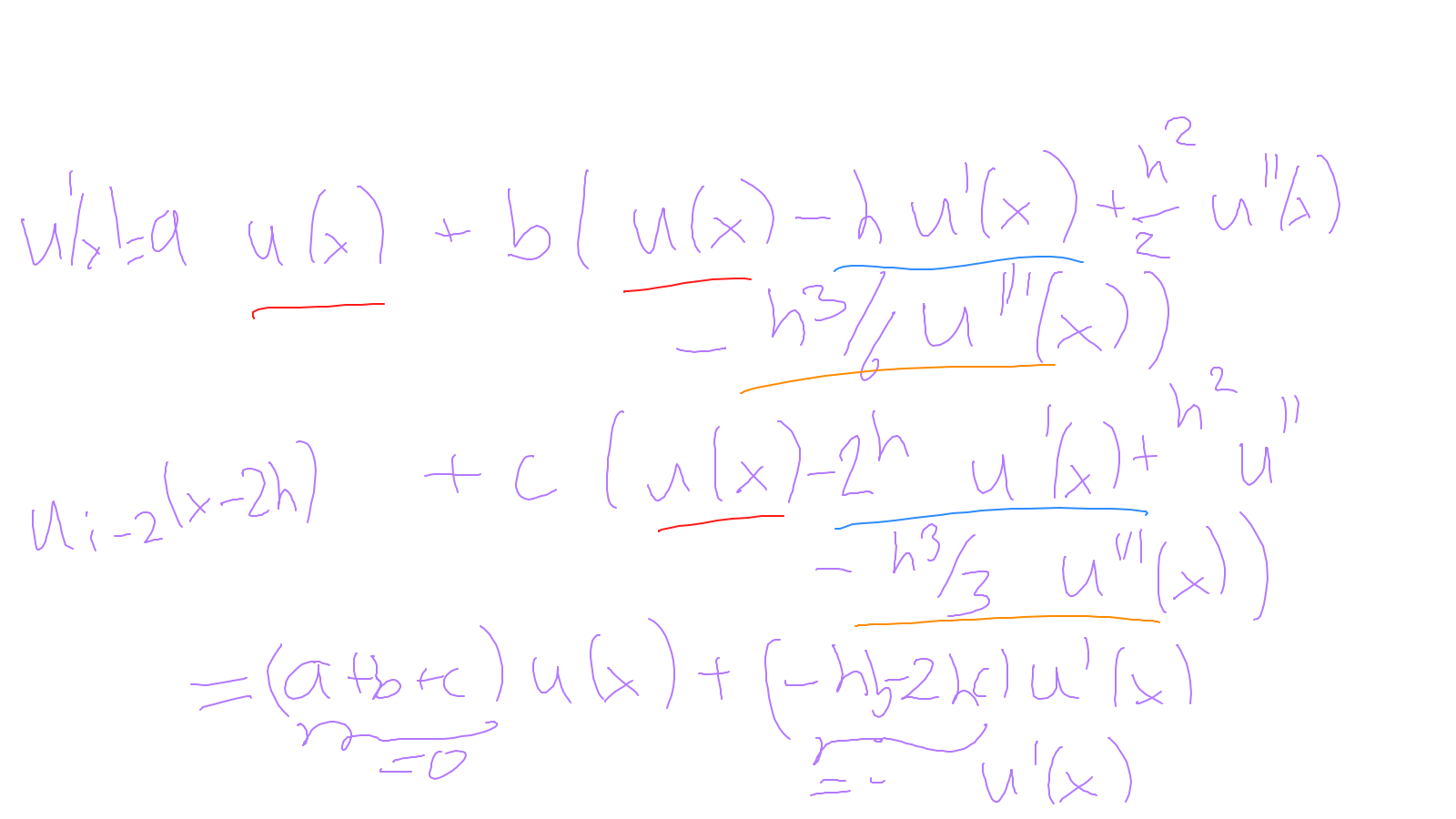
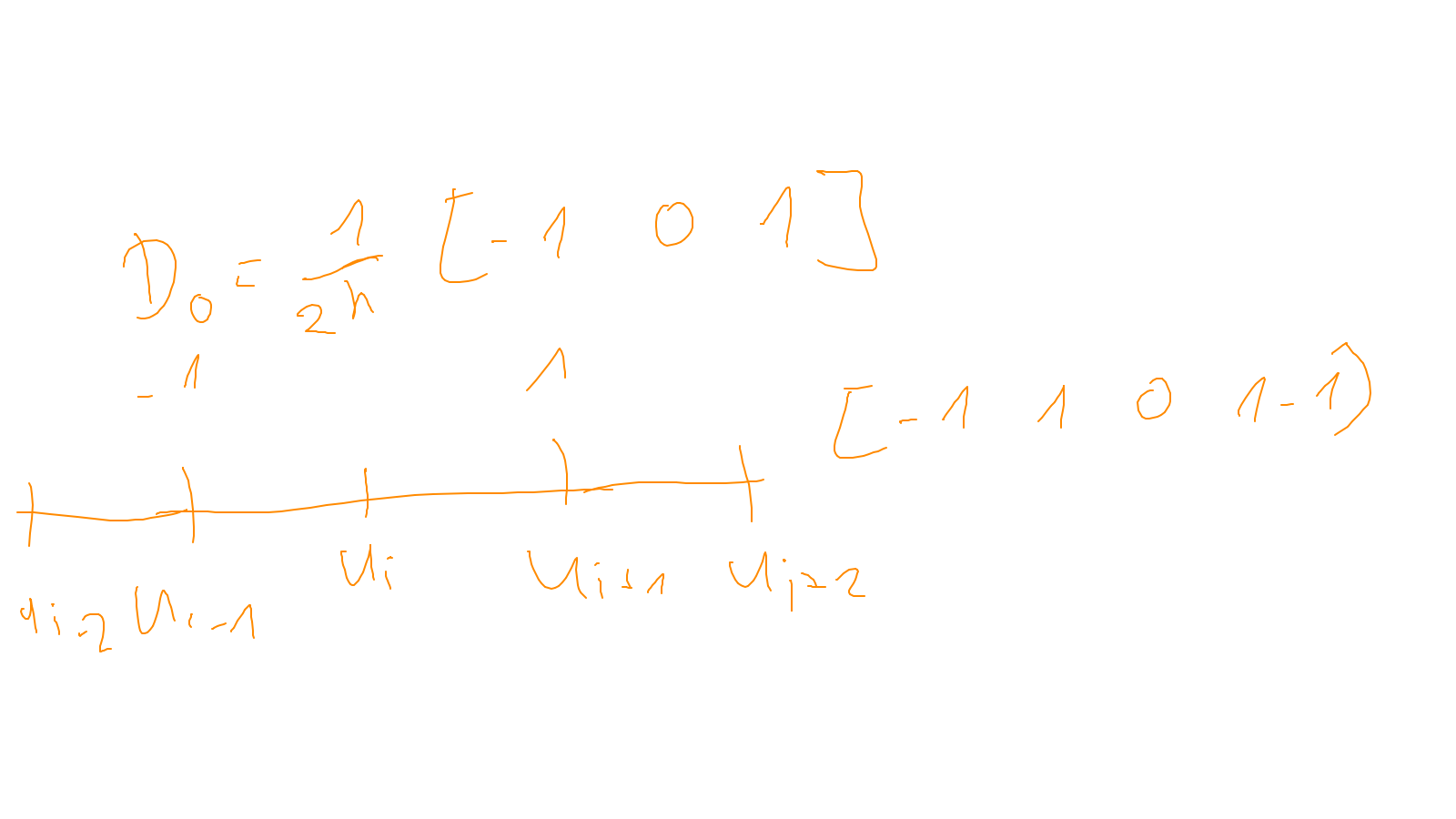
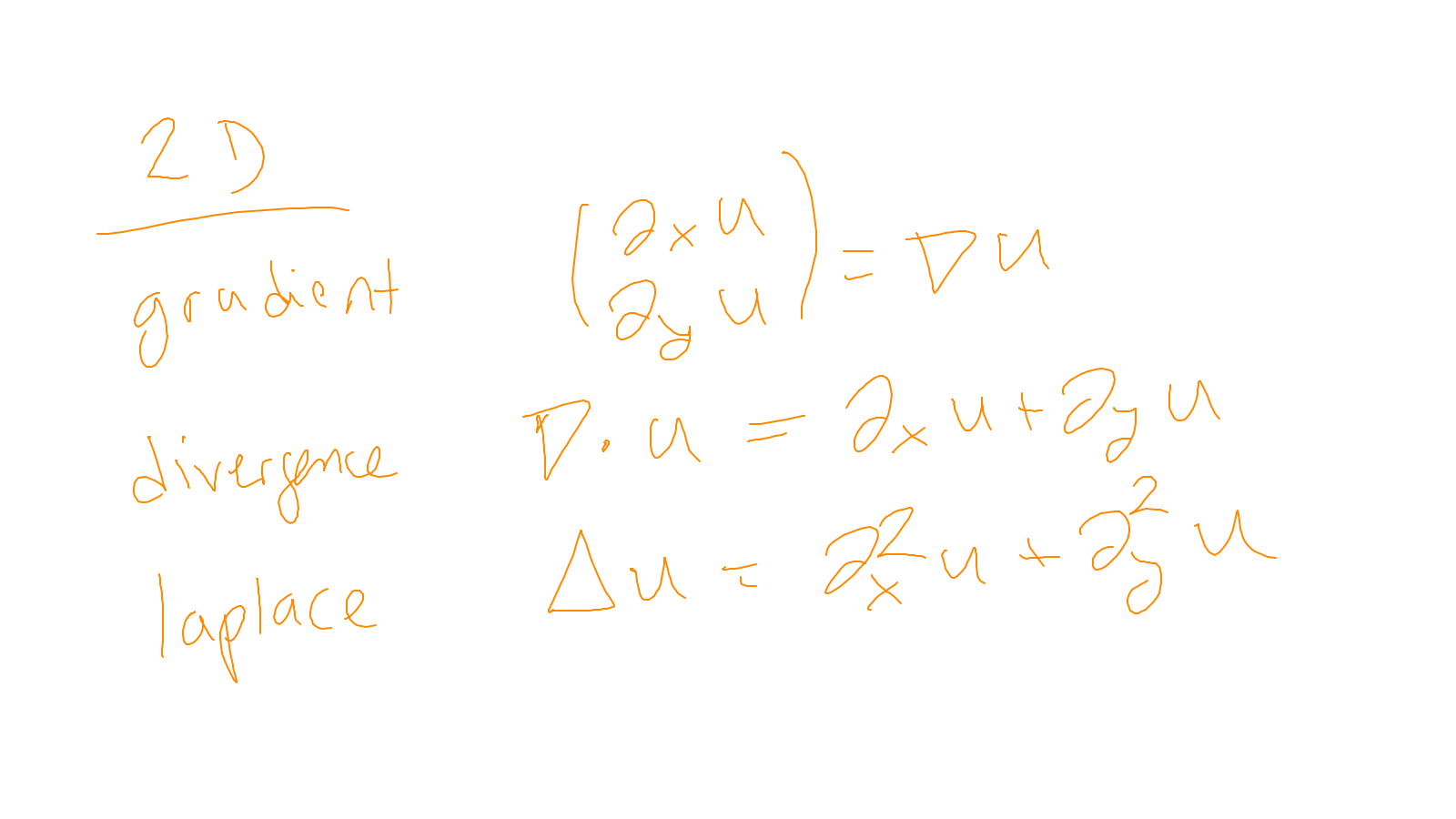
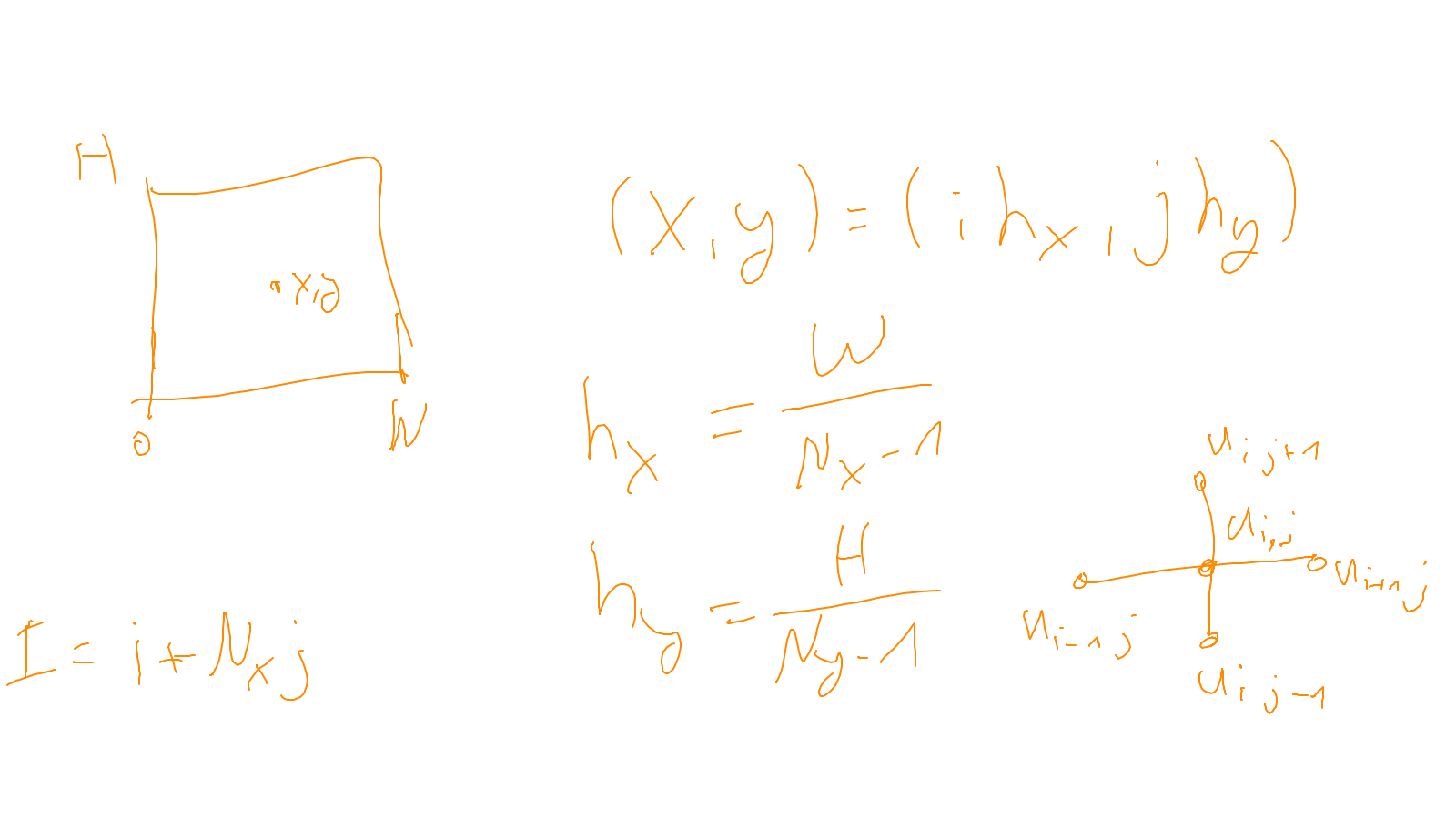
Lecture 4: smoothers #
In this lecture we will finish covering efficient matrix storage from: ipython notebook.
Alternatively, you can run the notebook online without installing python.
After that we will start discussing efficient solvers for linear systems. This lecture will cover smoothers: ipython notebook.
Alternatively, you can run the notebook online without installing python.
After the lecture have a look at the corresponding exercise.
The video is now available at: video
The content of the whiteboard can be found below. It is also all contained in the ipython notebook itself.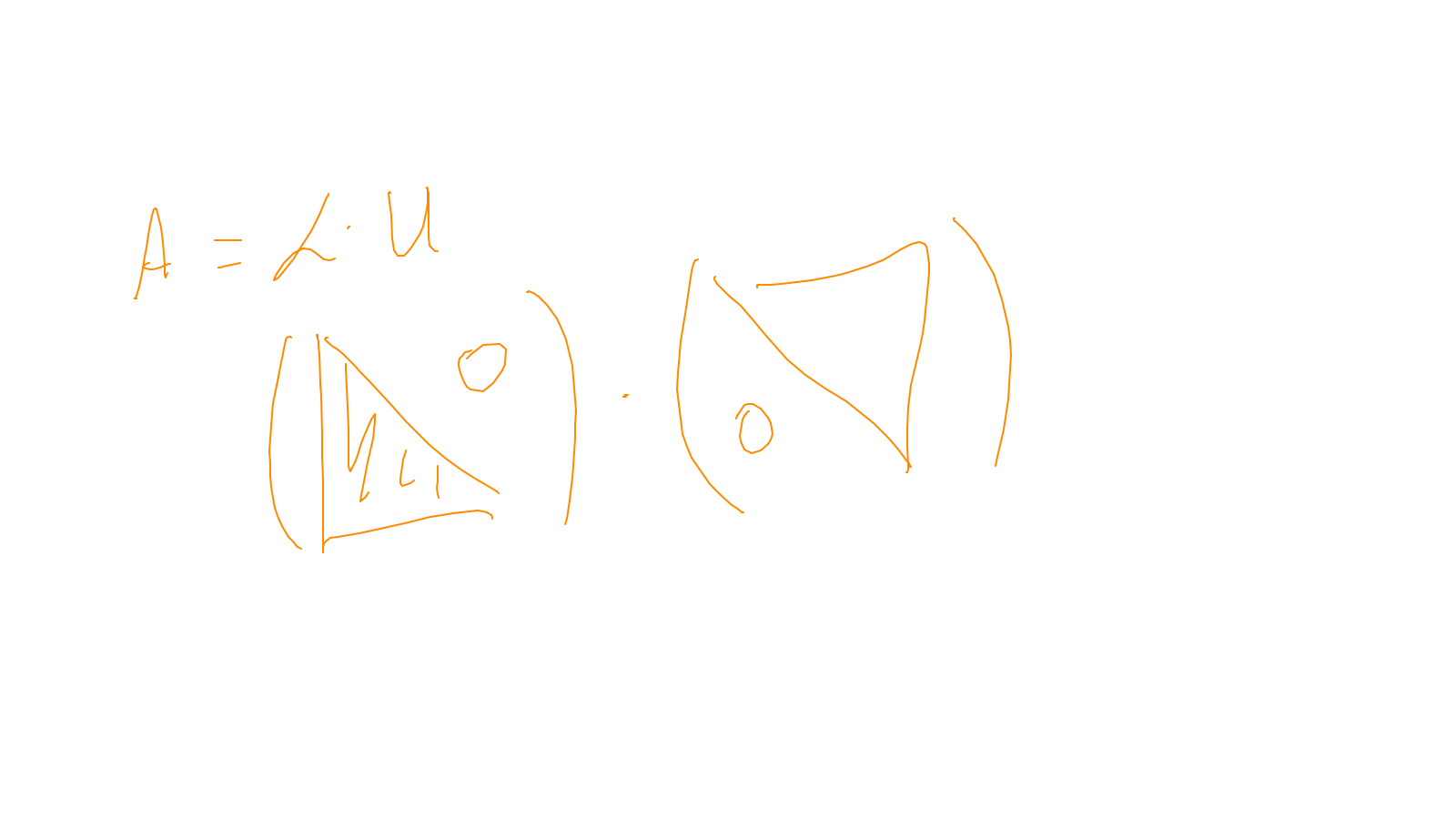
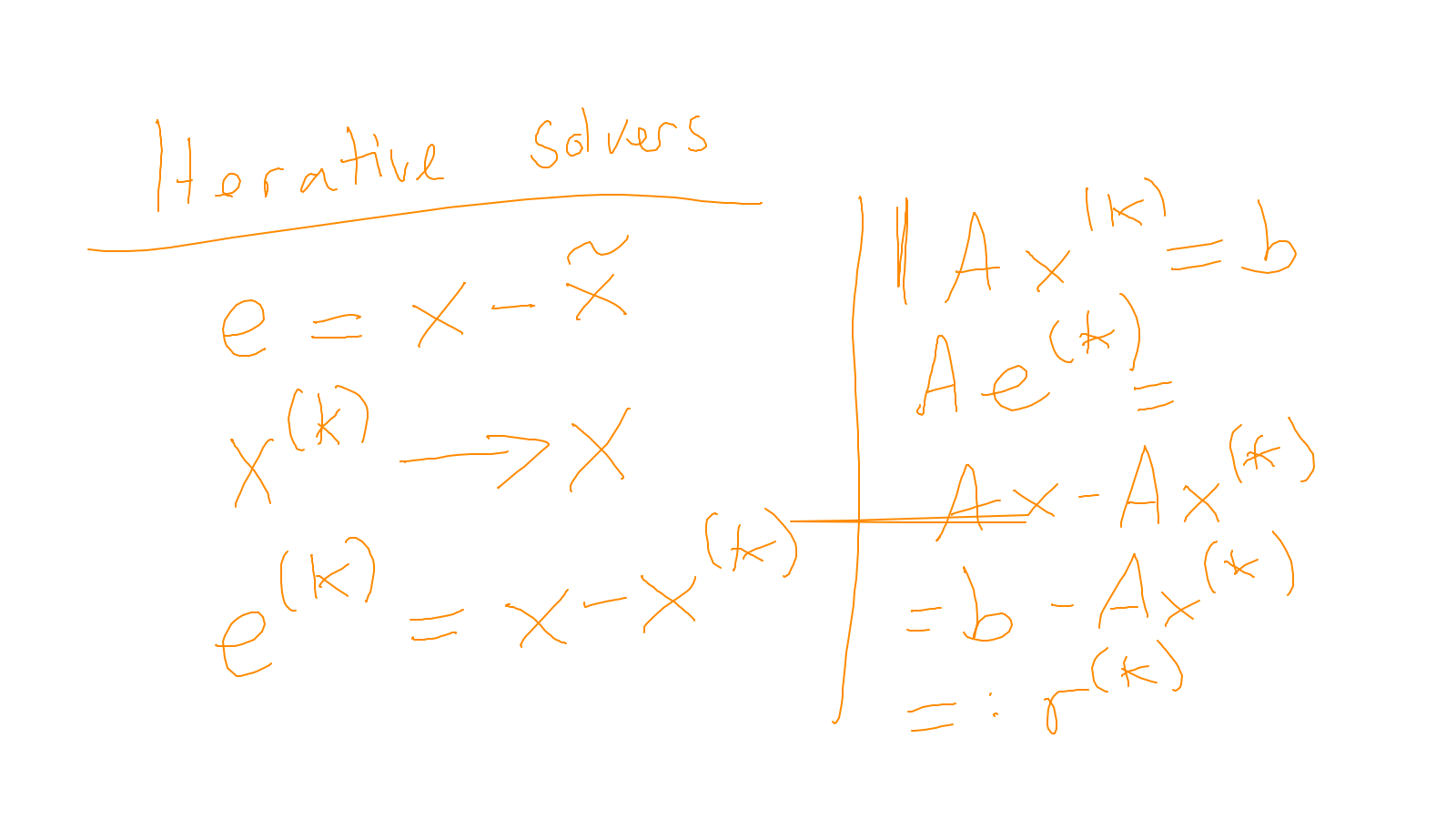
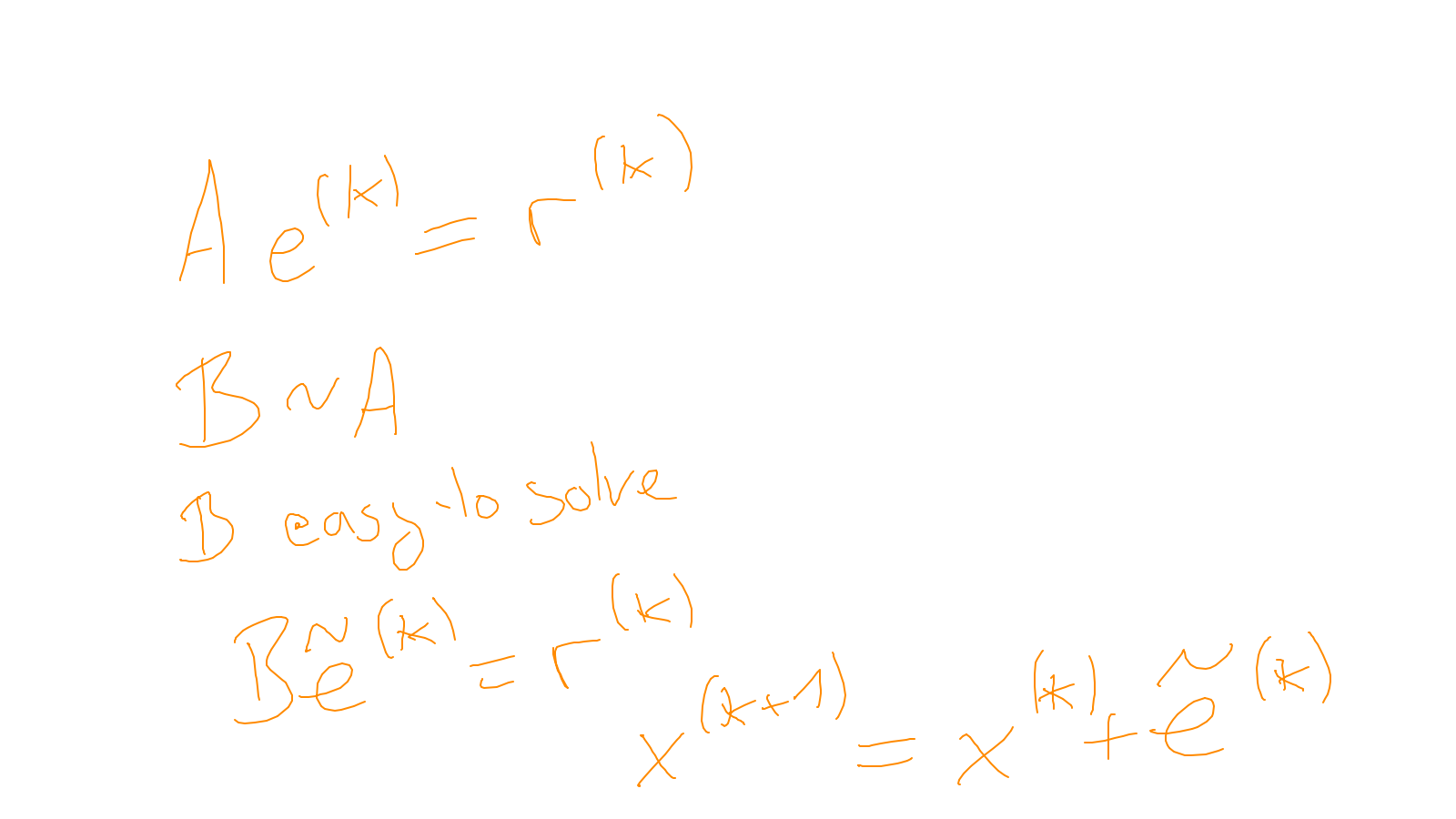
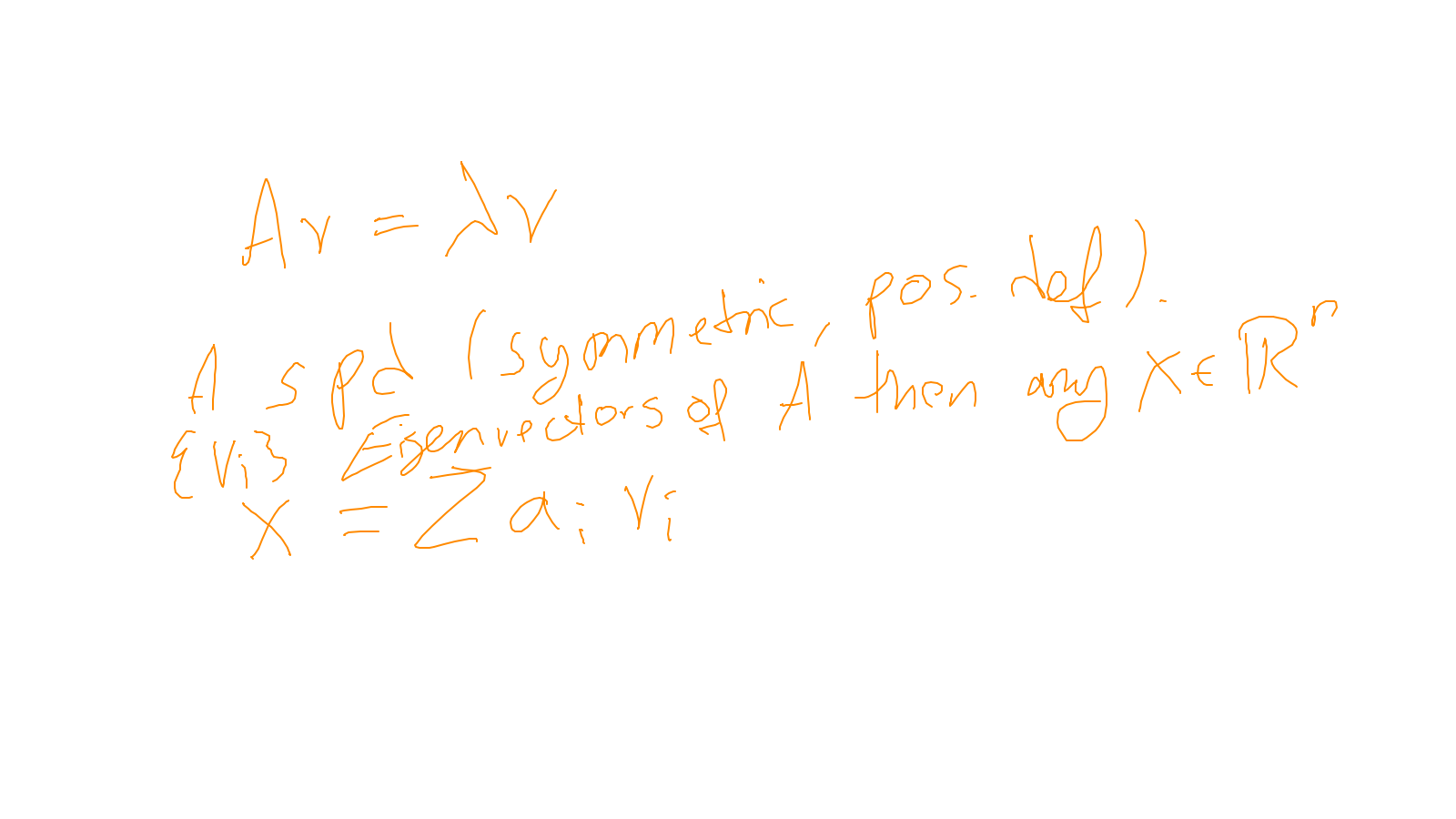
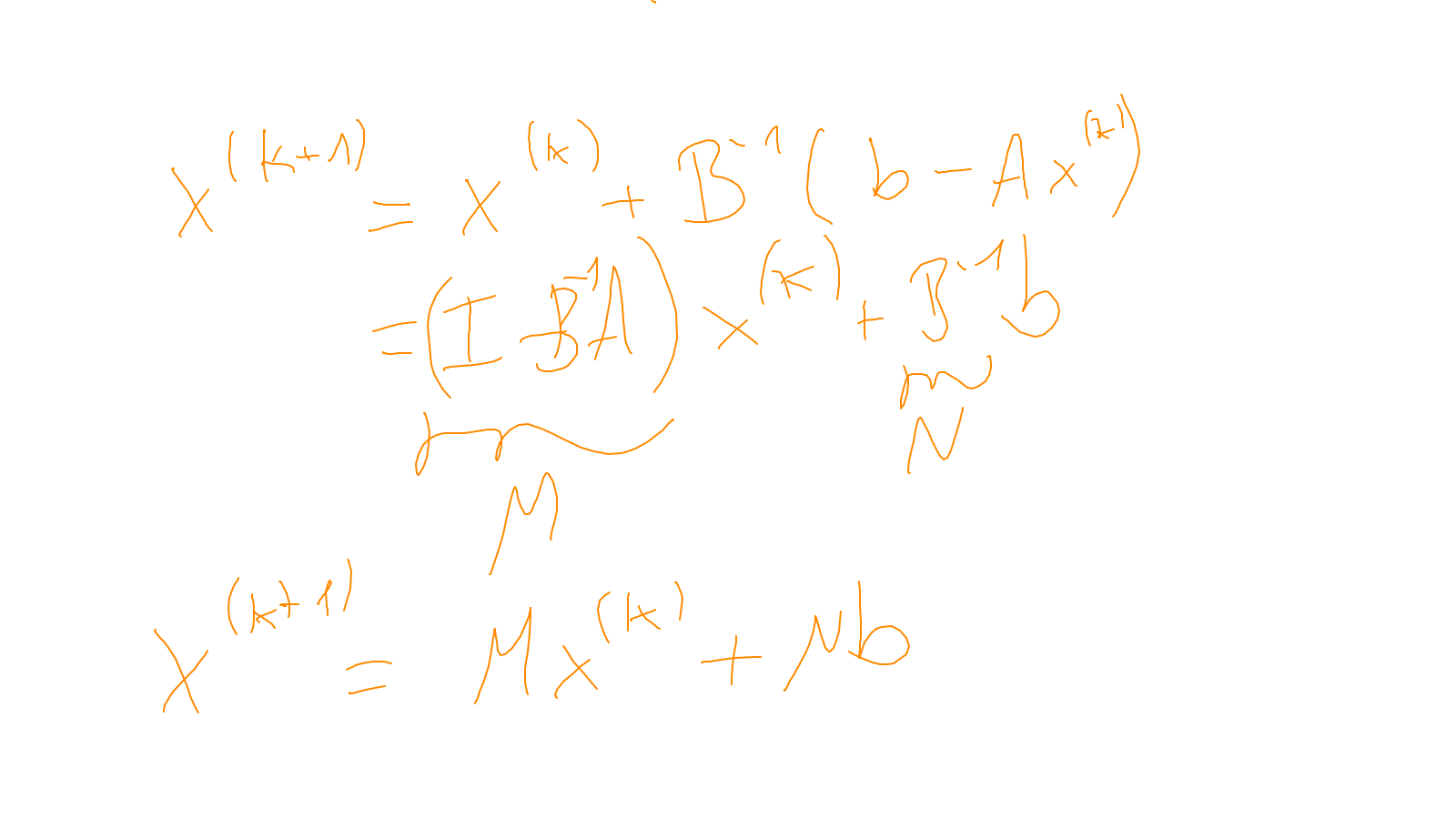
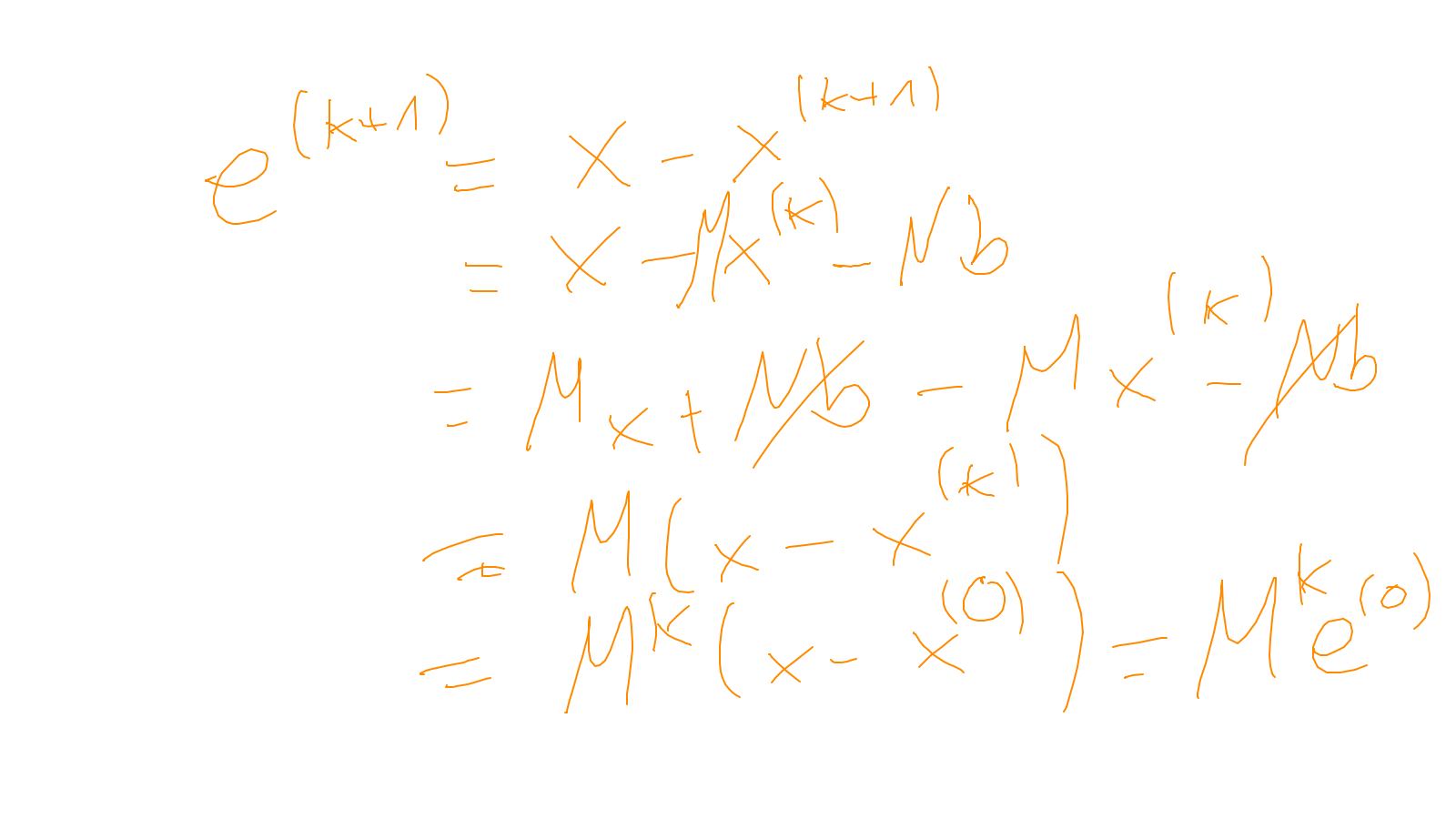
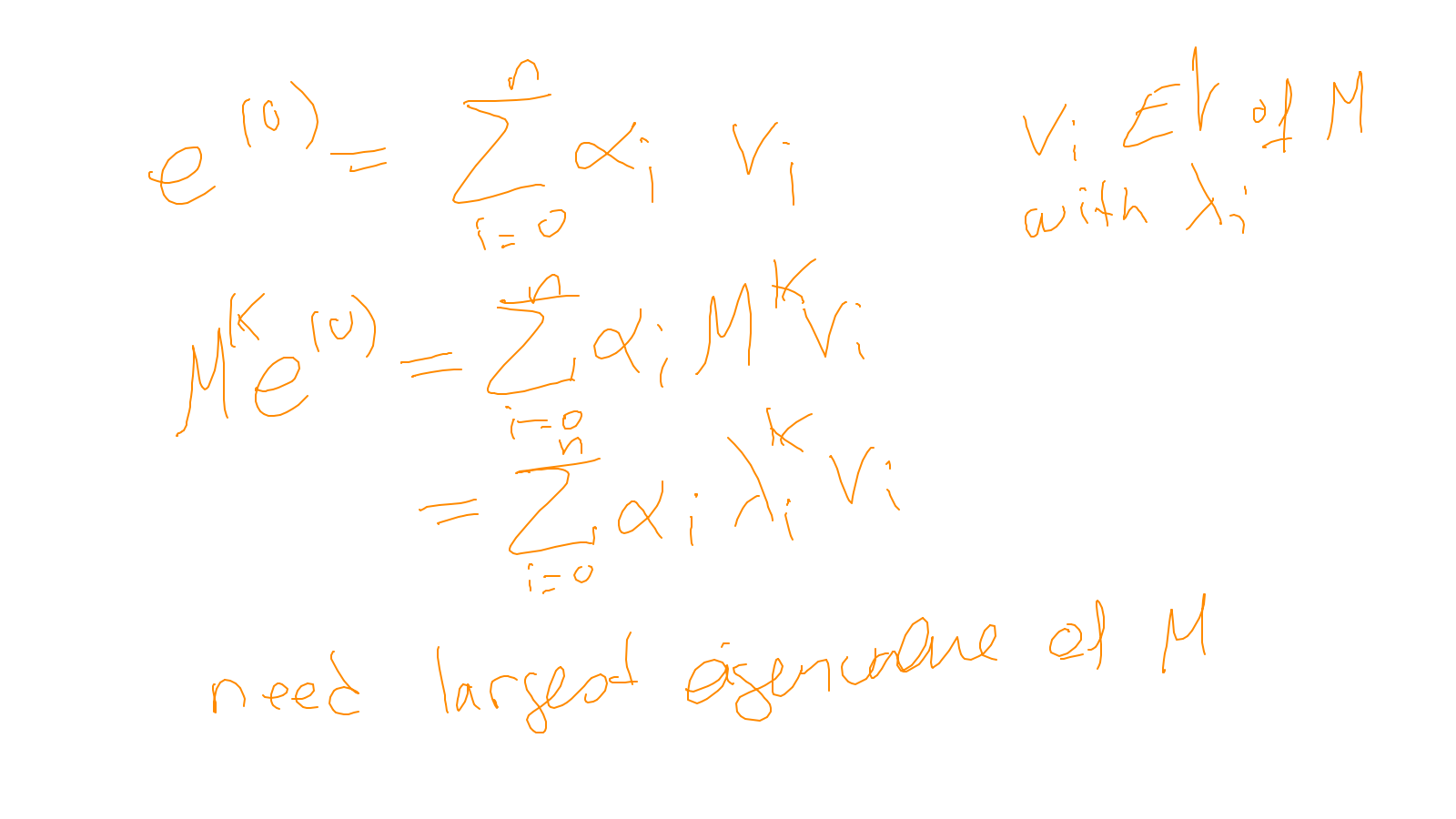
Lecture 5: smoothers #
This lecture will cover smoothers: ipython notebook.
Alternatively, you can run the notebook online without installing python.
We also started on the multigrid method: ipython notebook
The video is now available at: video
The content of the whiteboard can be found below. It is also all contained in the ipython notebook itself.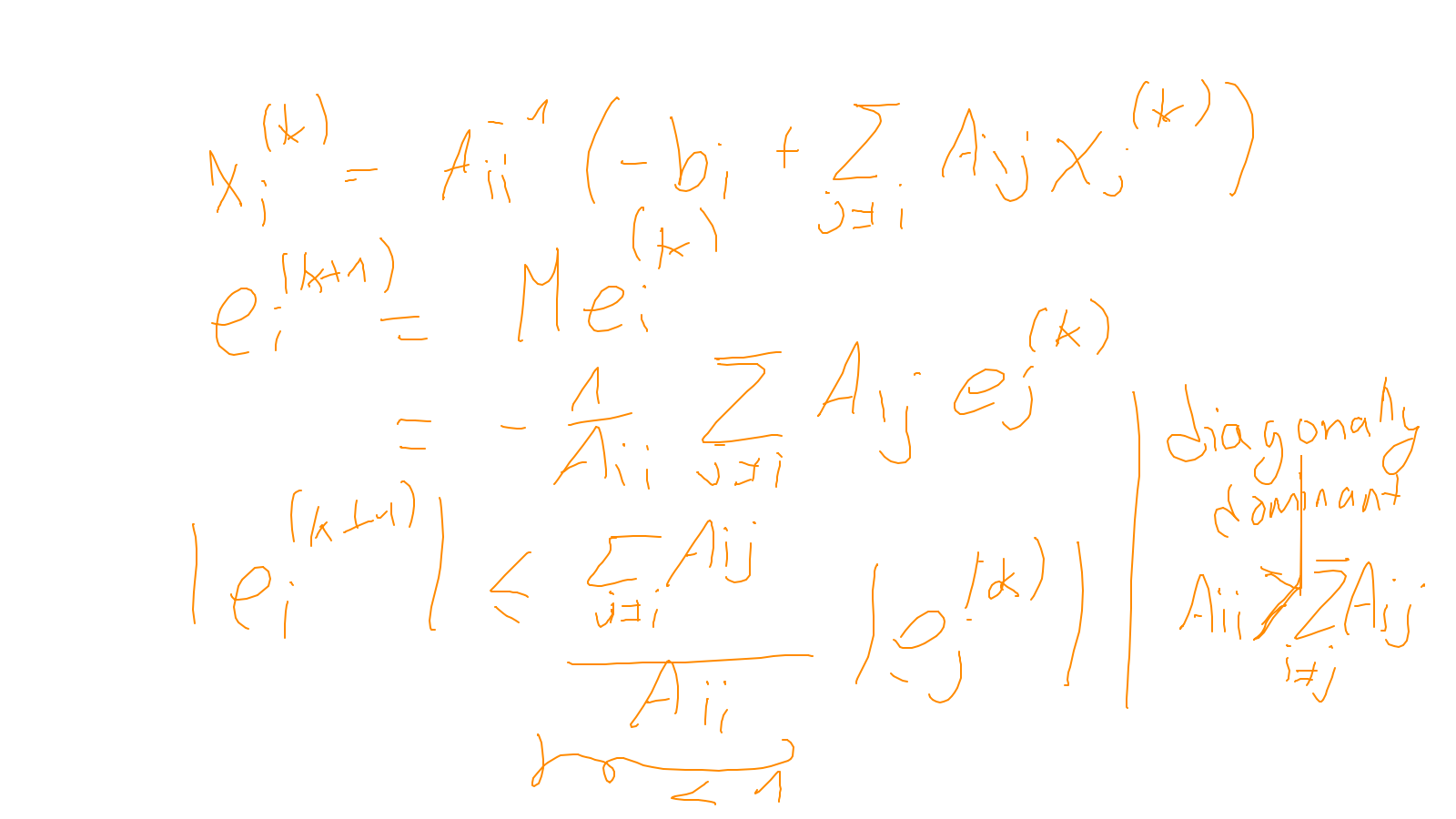
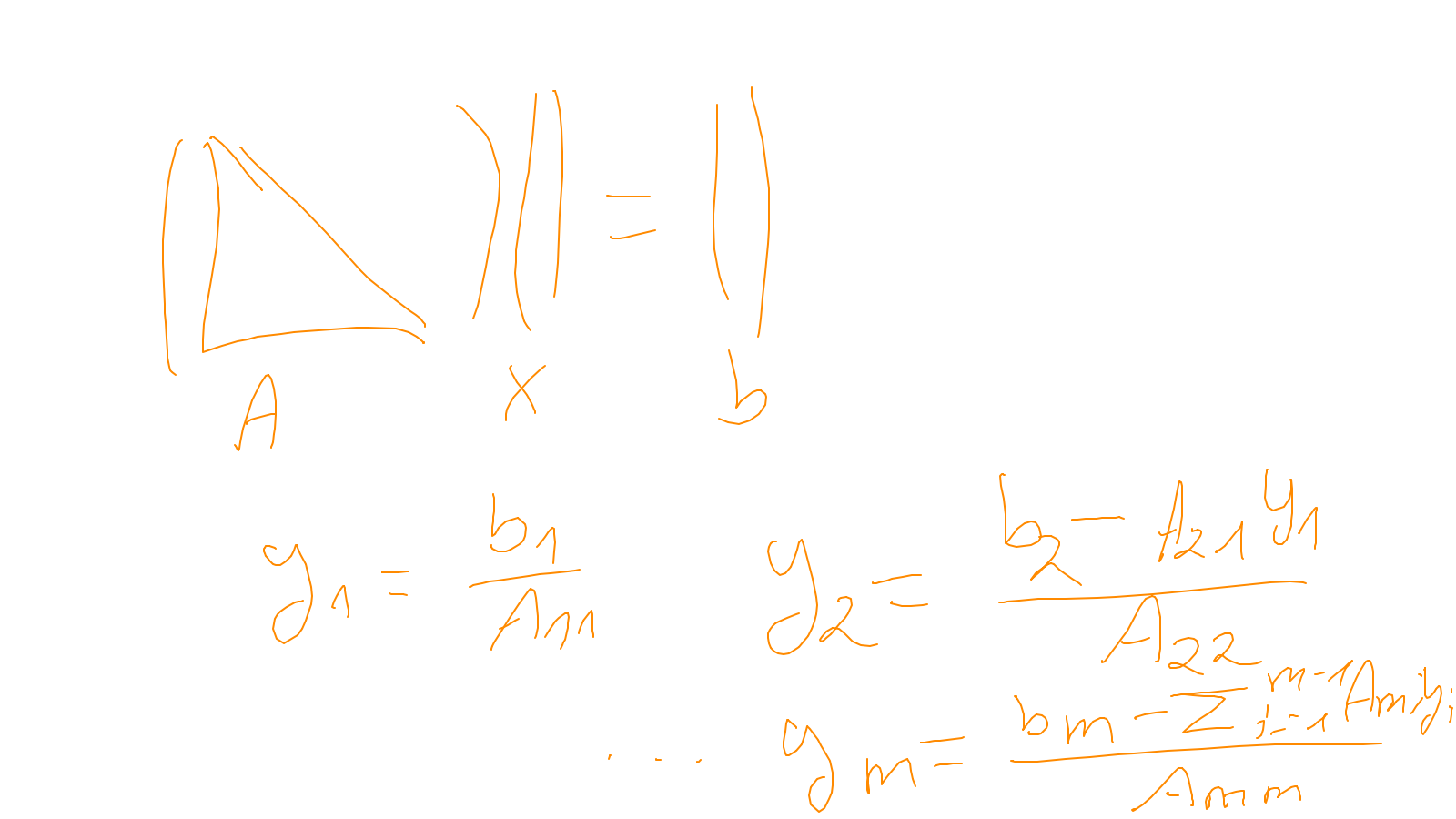
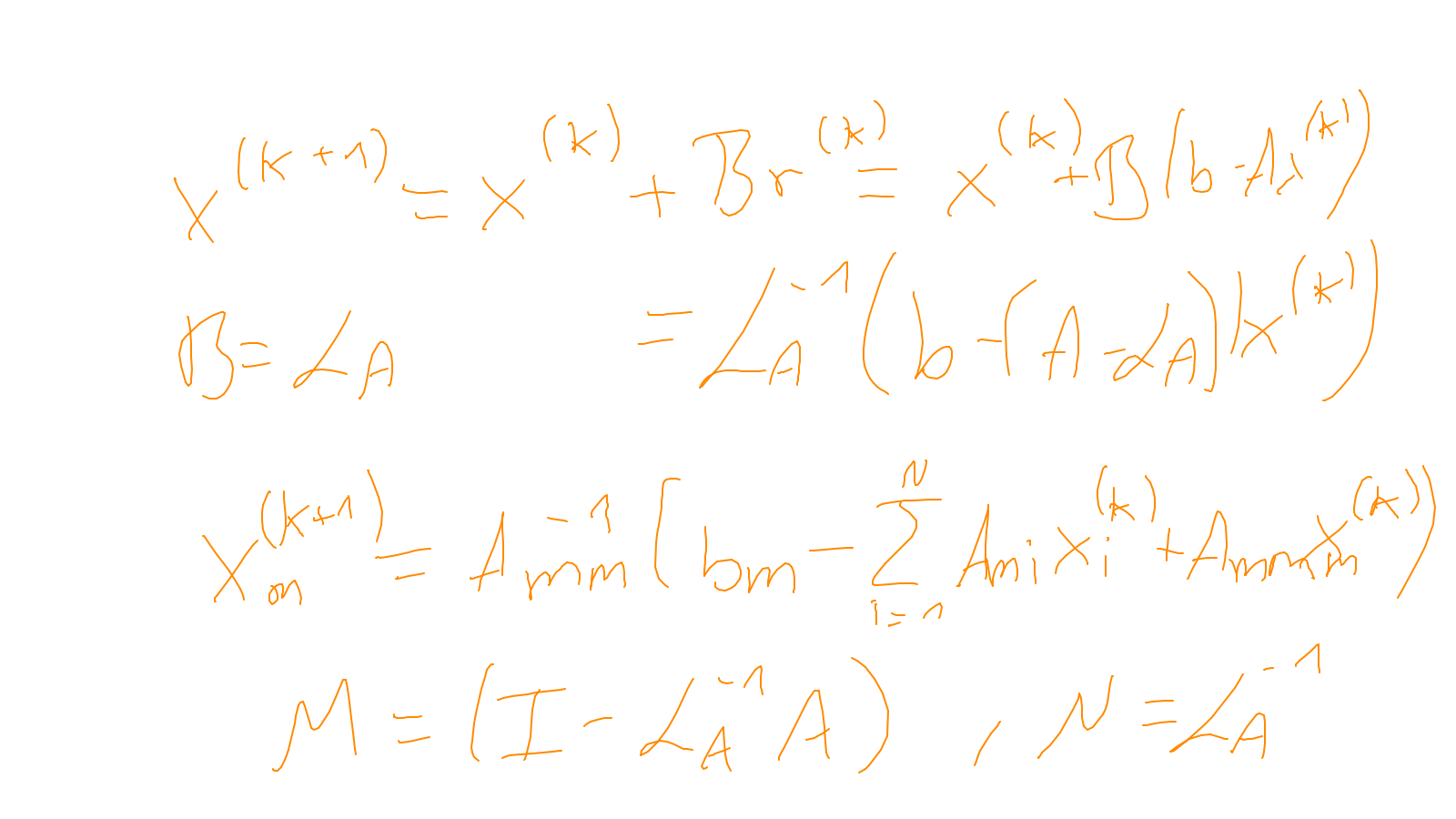
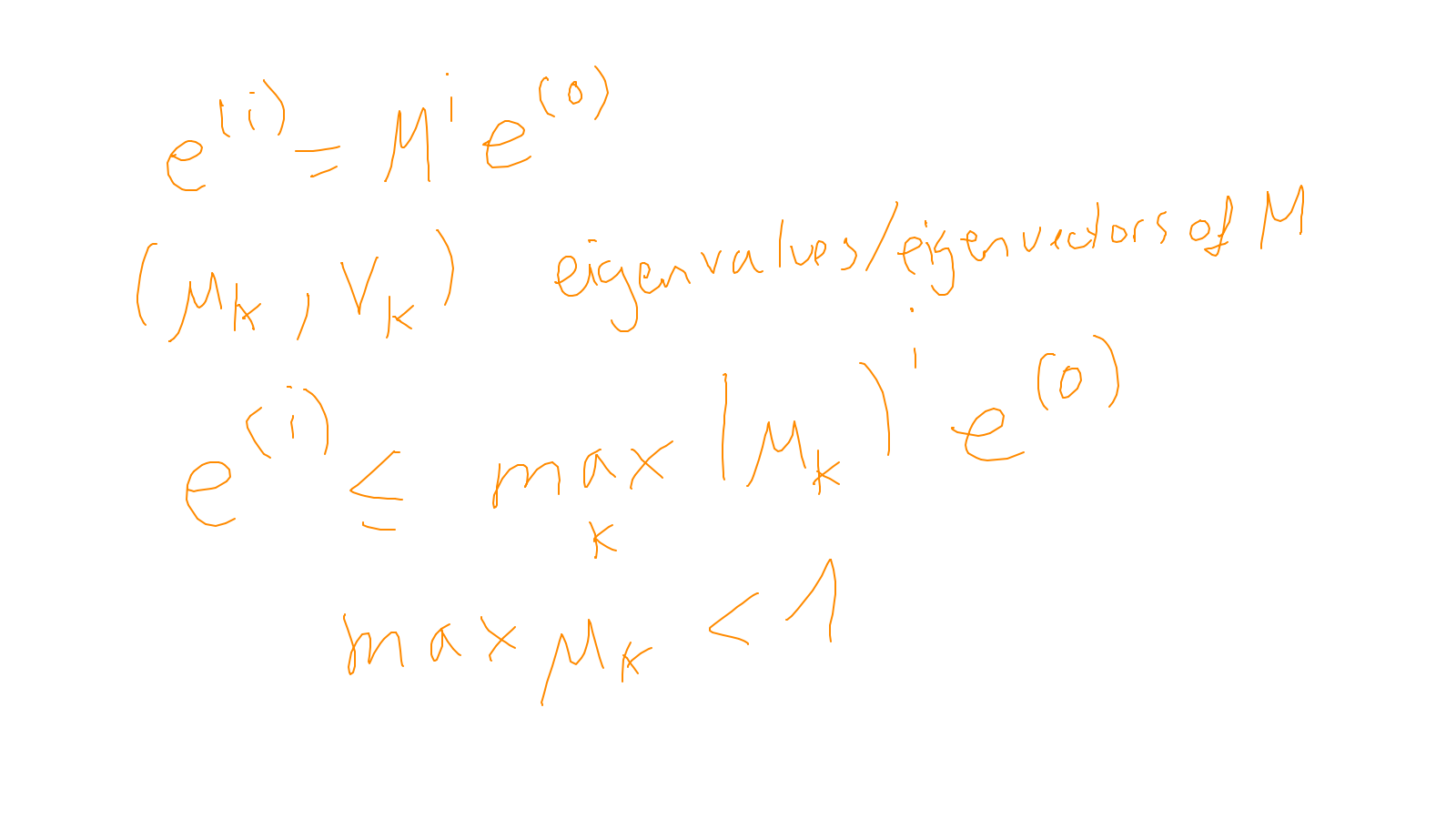
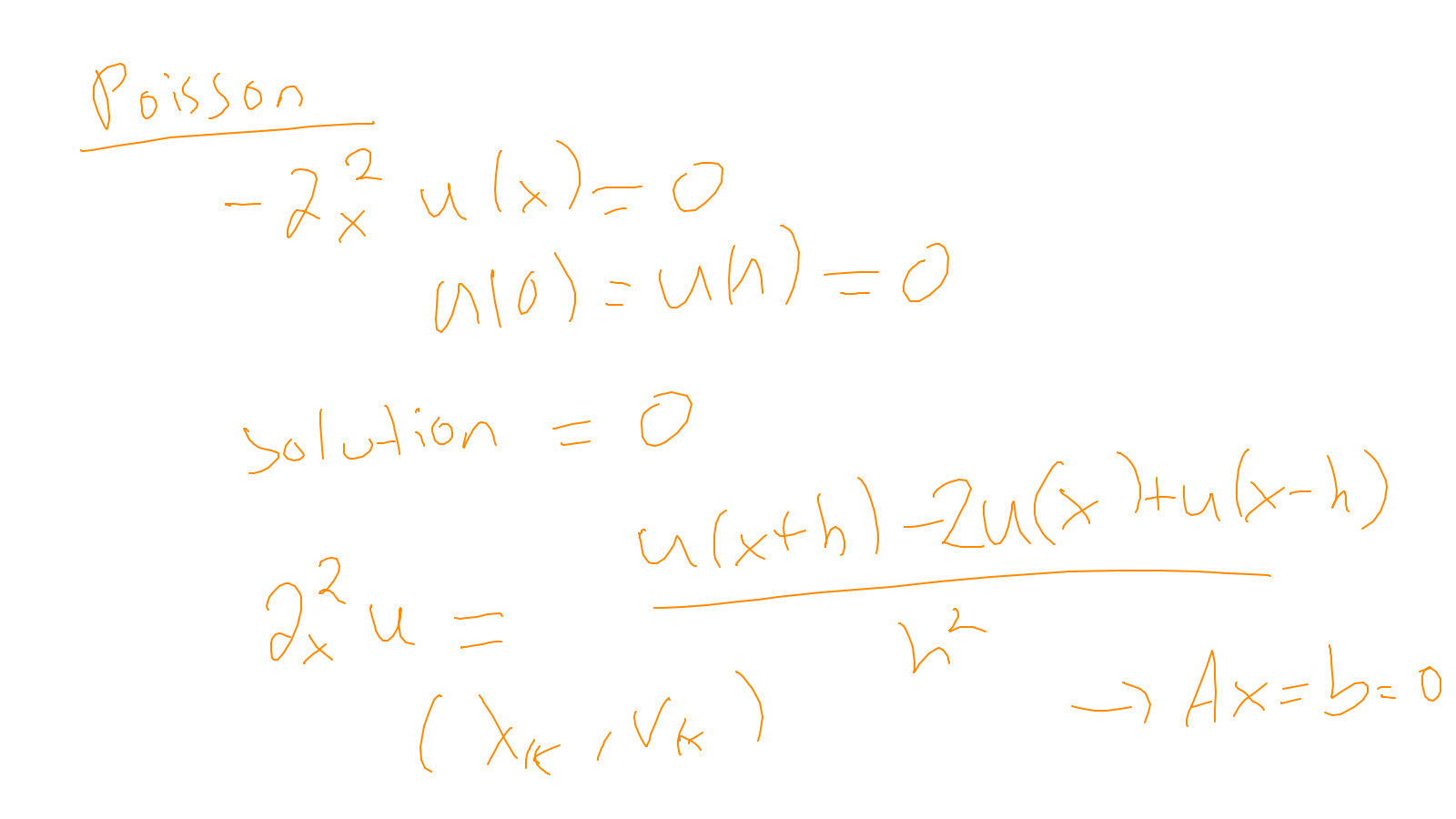
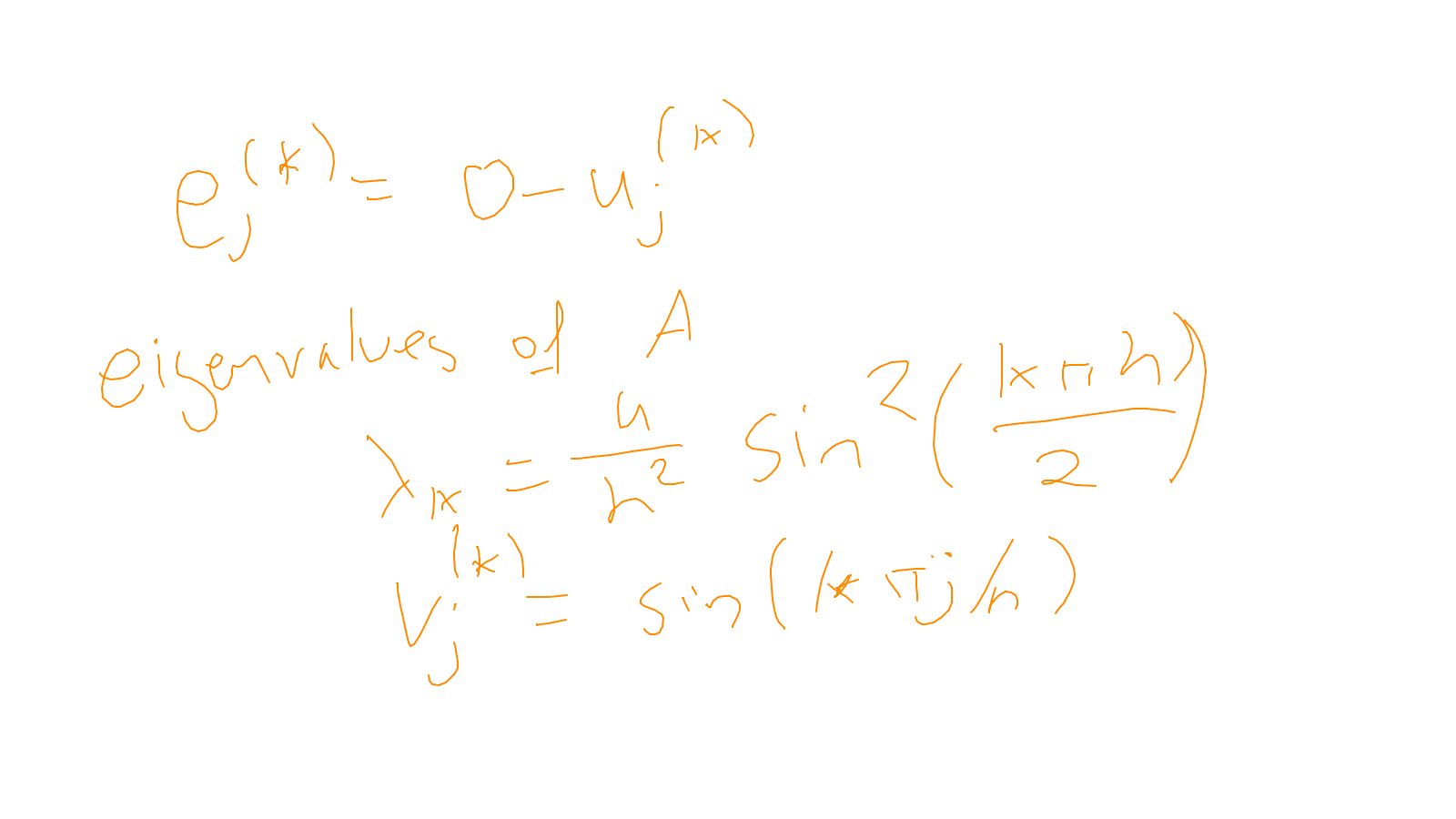
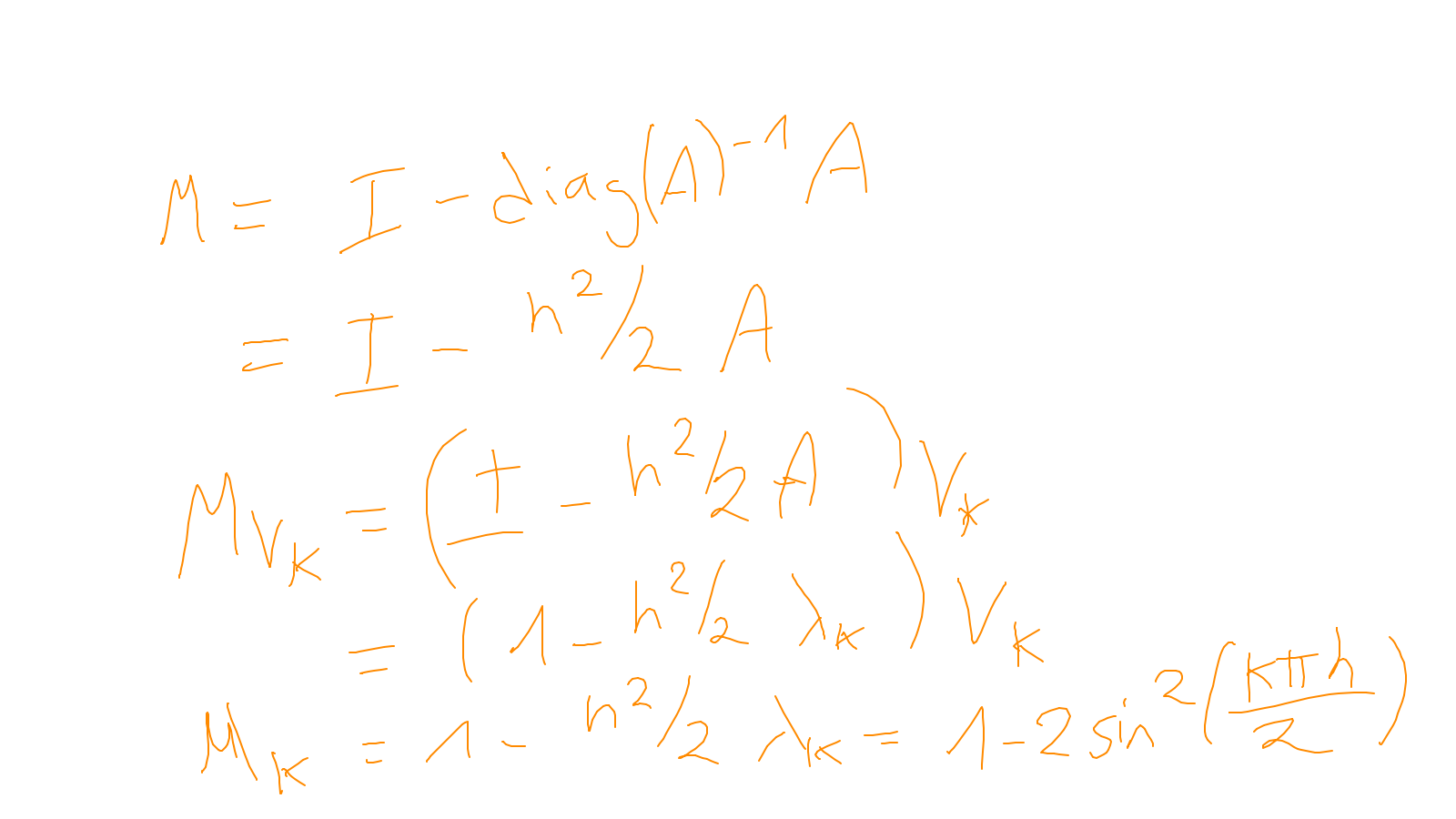
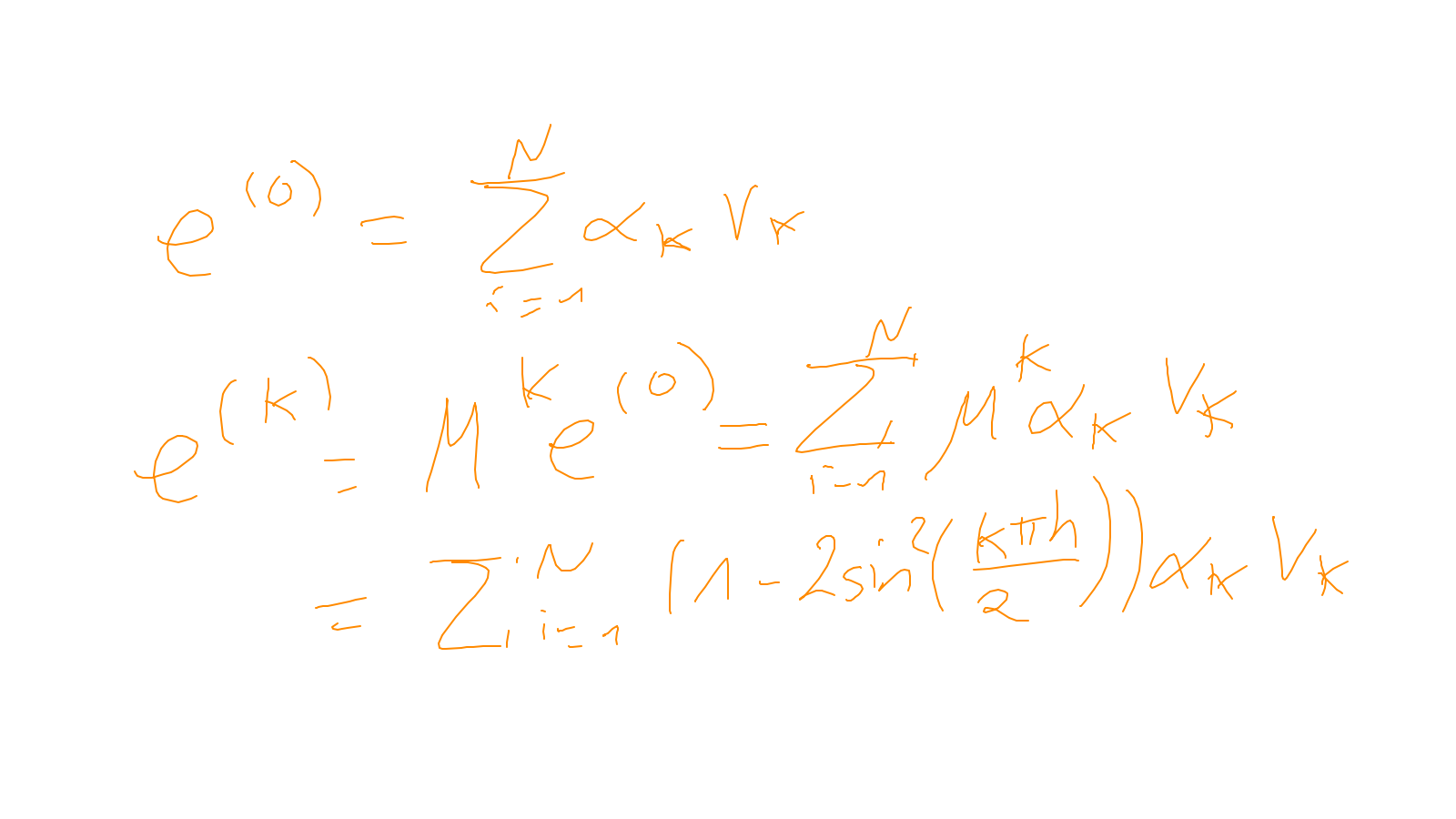
Lecture 6: multigrid #
We continue with the multigrid method: ipython notebook
The video is now available at: video
The content of the whiteboard can be found below. It is also all contained in the ipython notebook itself.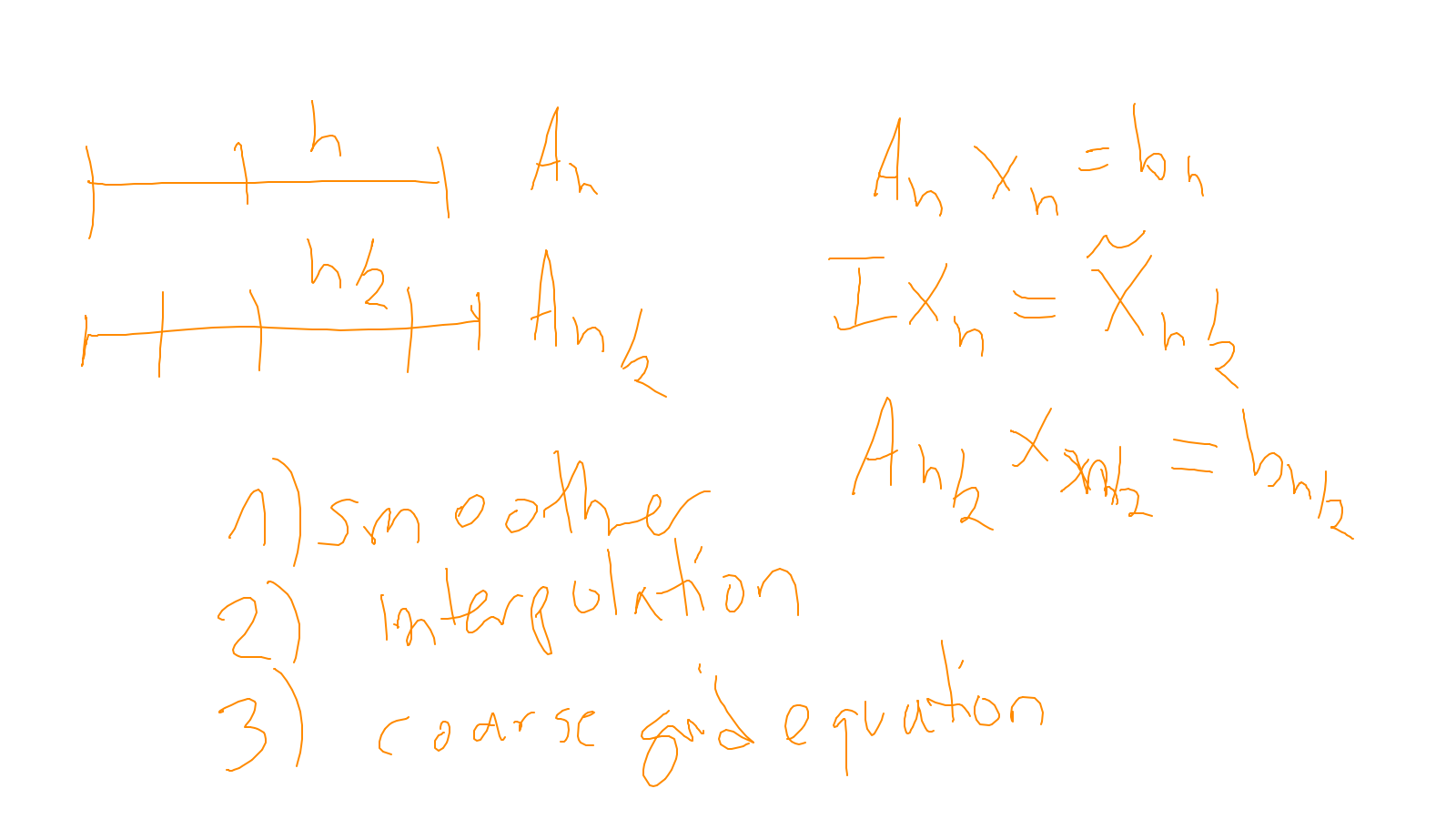
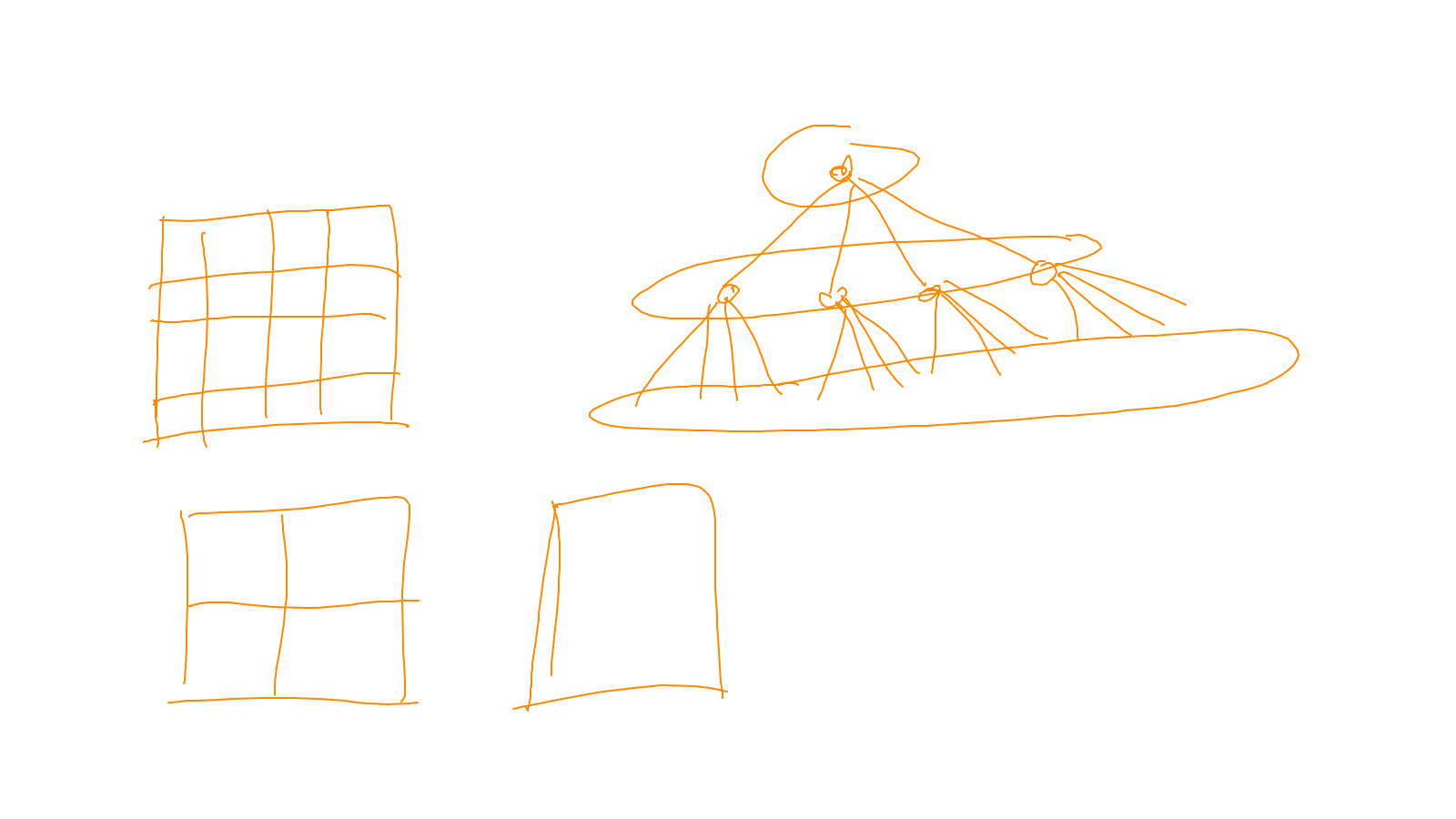
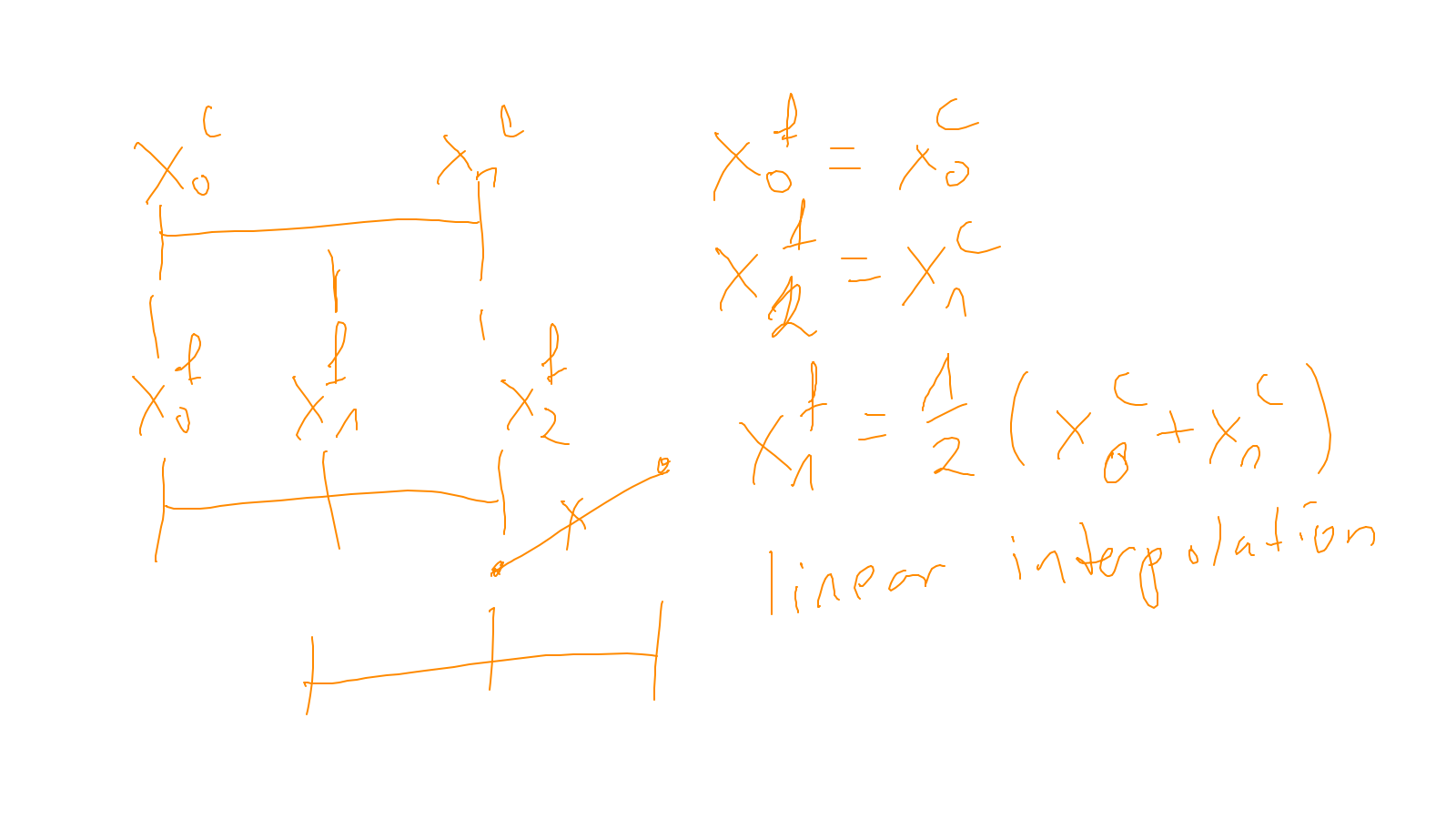

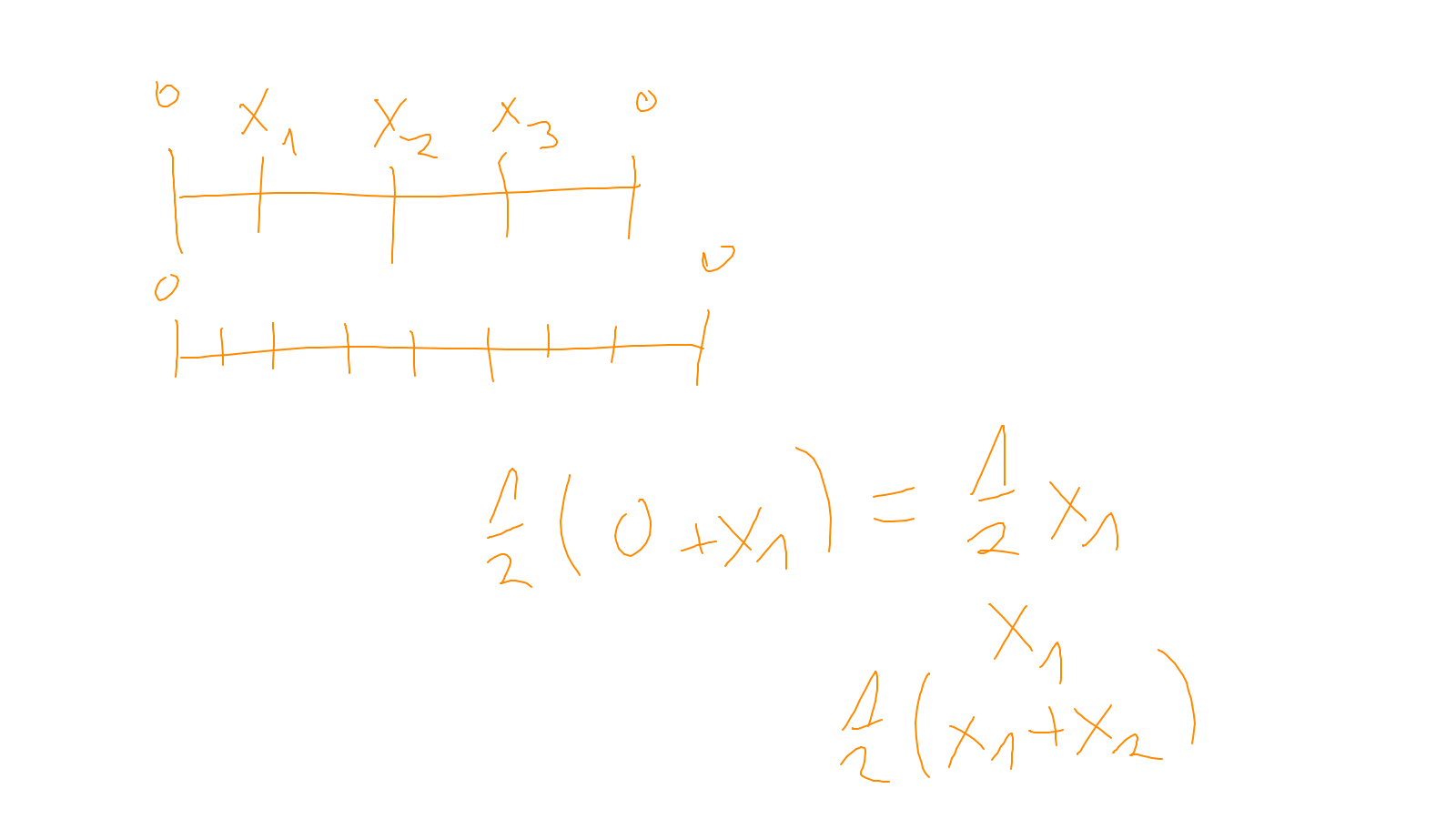
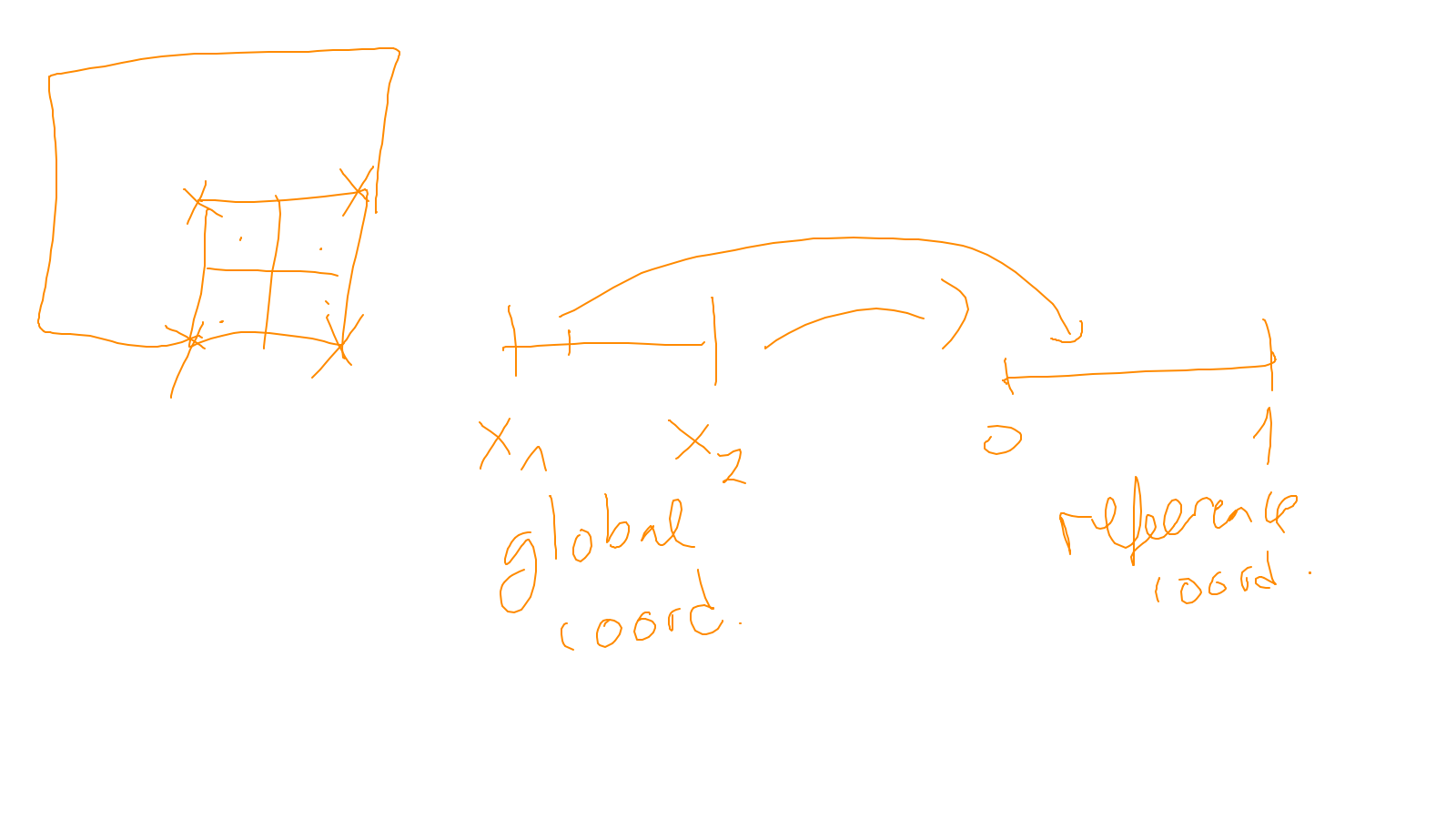
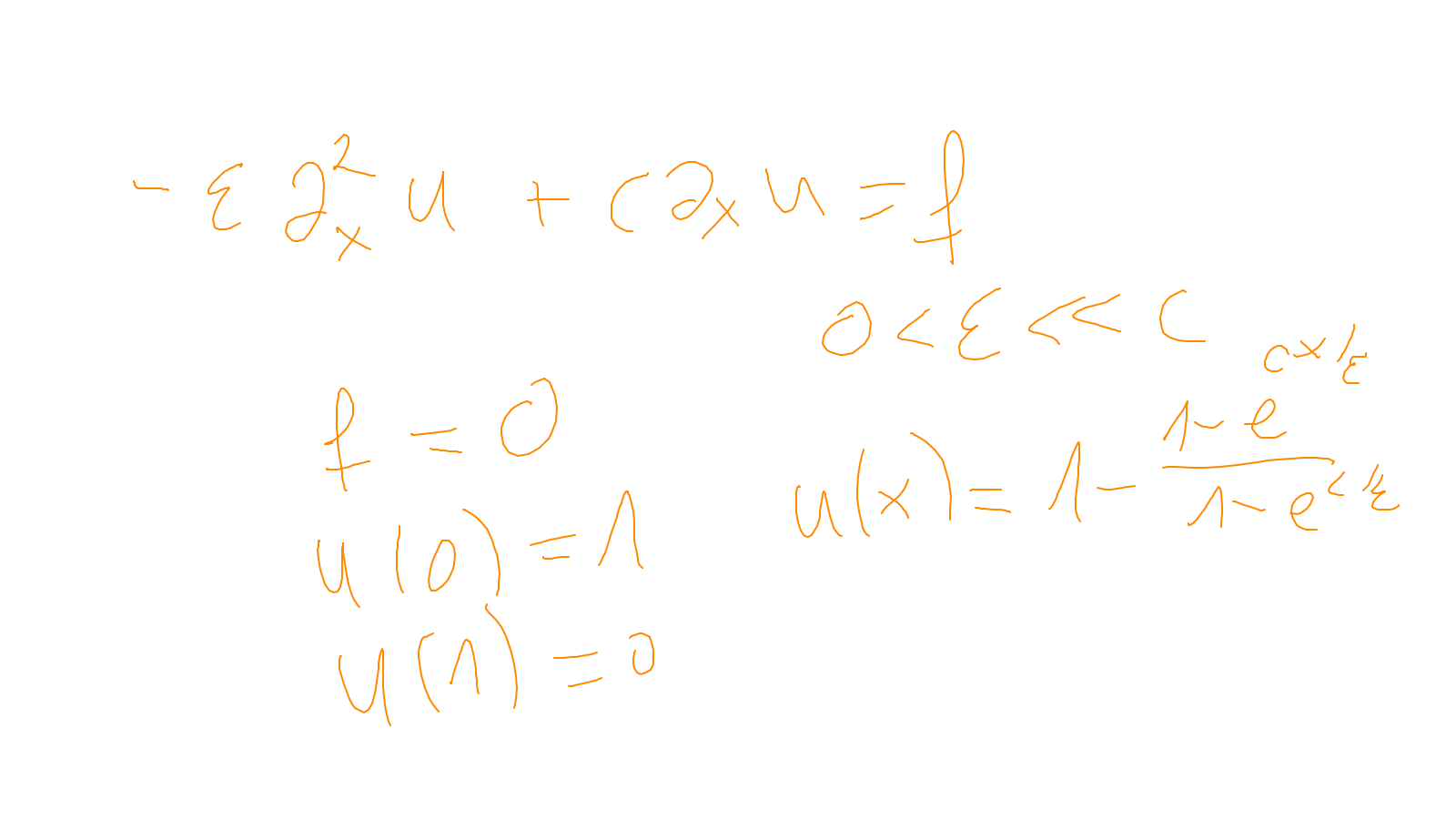
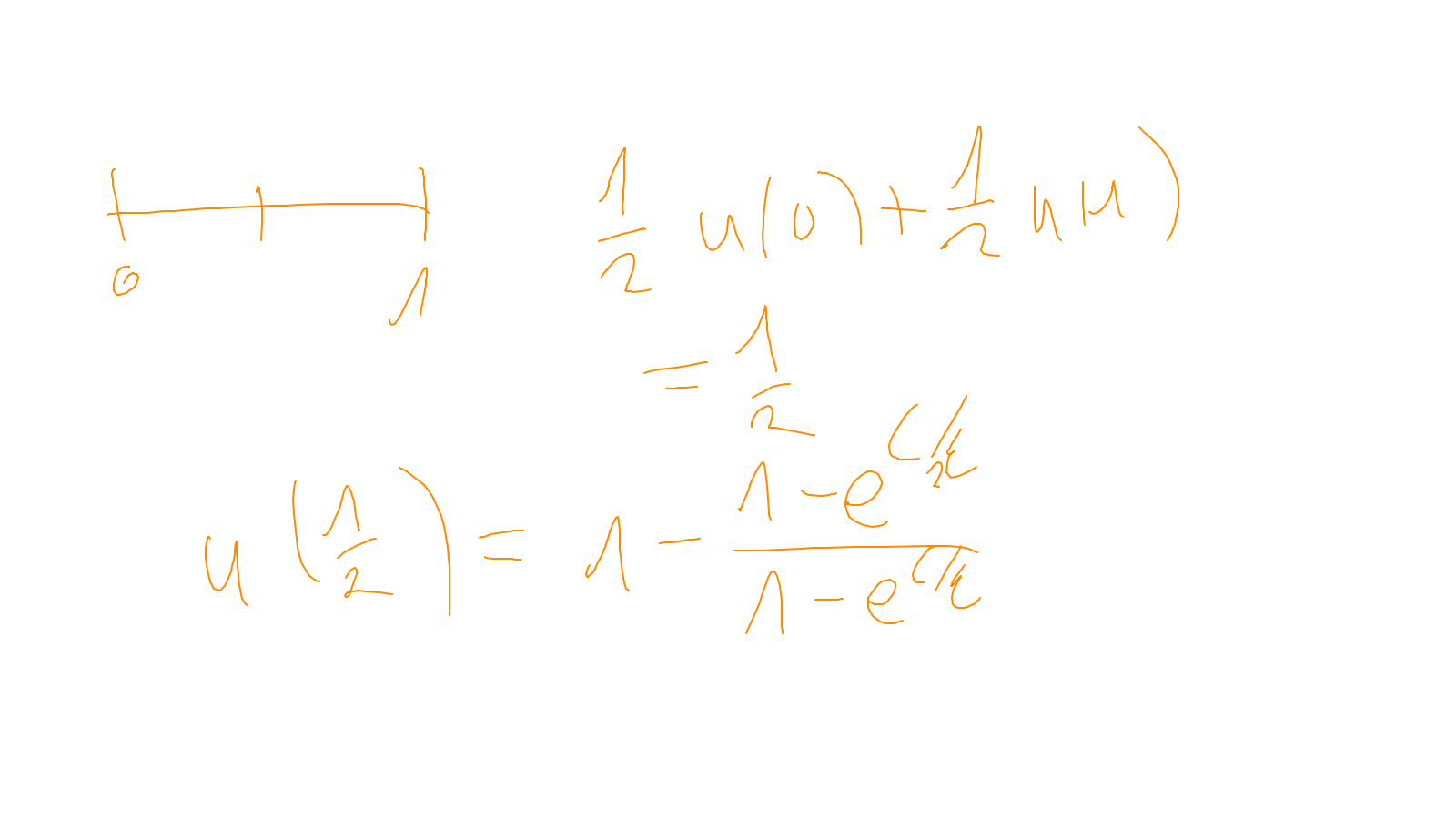
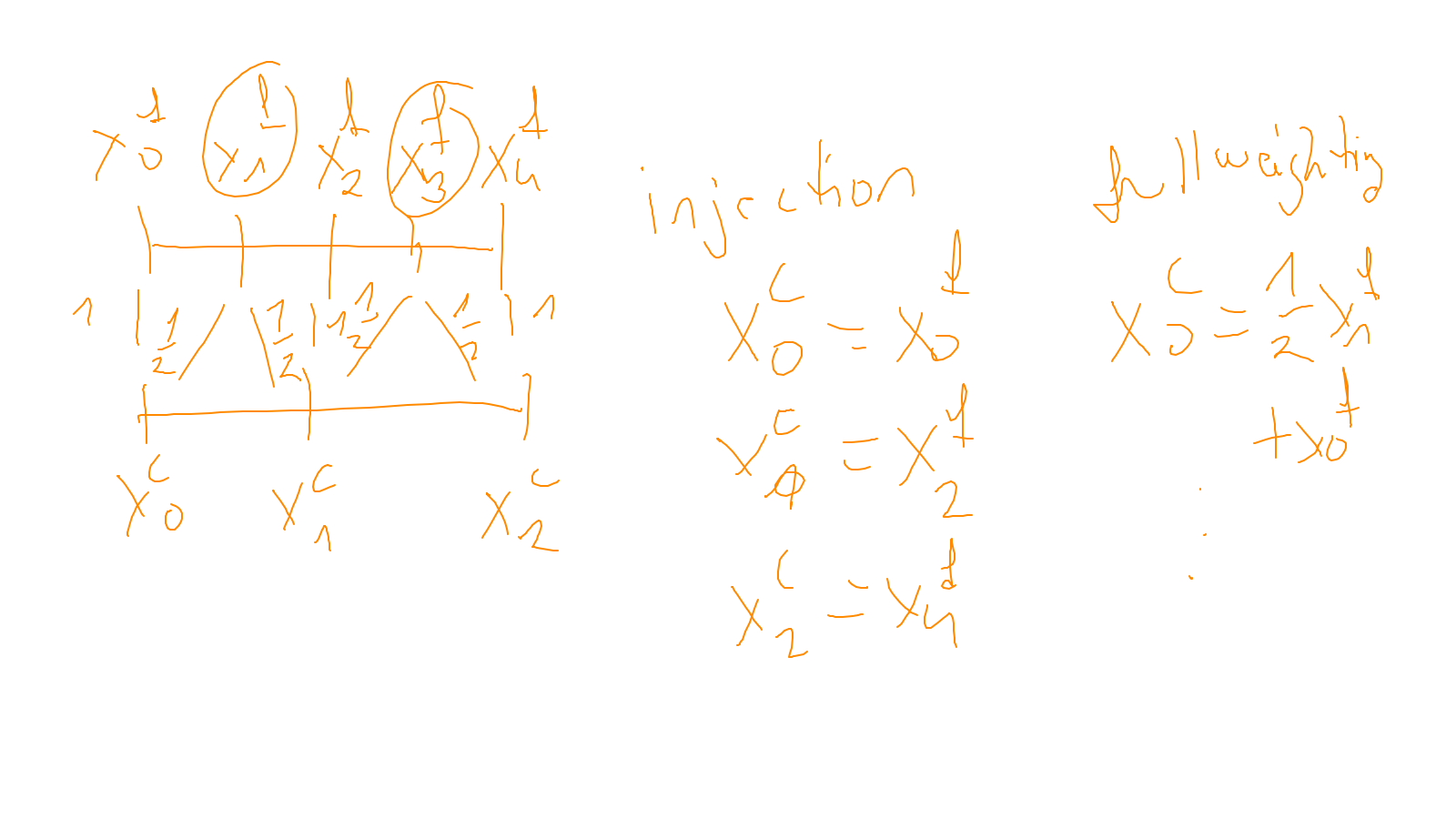
Lecture 7: multigrid #
We continue with the multigrid method: ipython notebook
The proof for Poisson can be found in:
- Dietrich Braess and Wolfgang Hackbusch,A New Convergence Proof for the Multi-grid Method including the V-Cycle, SIAM J. Numer. Anal.,20, 967–975, 1983
At this point you may want to have a look at the two exercises:
- On two grid: exercise. If you are unused to Fourier-analysis you will find this exercise quite challenging.
- and on the construction of the coarse grid operator: exercise
If you run into any issues, as always, feel free to ask.
The video is now available at: video
The content of the whiteboard can be found below. It is also all contained in the ipython notebook itself.
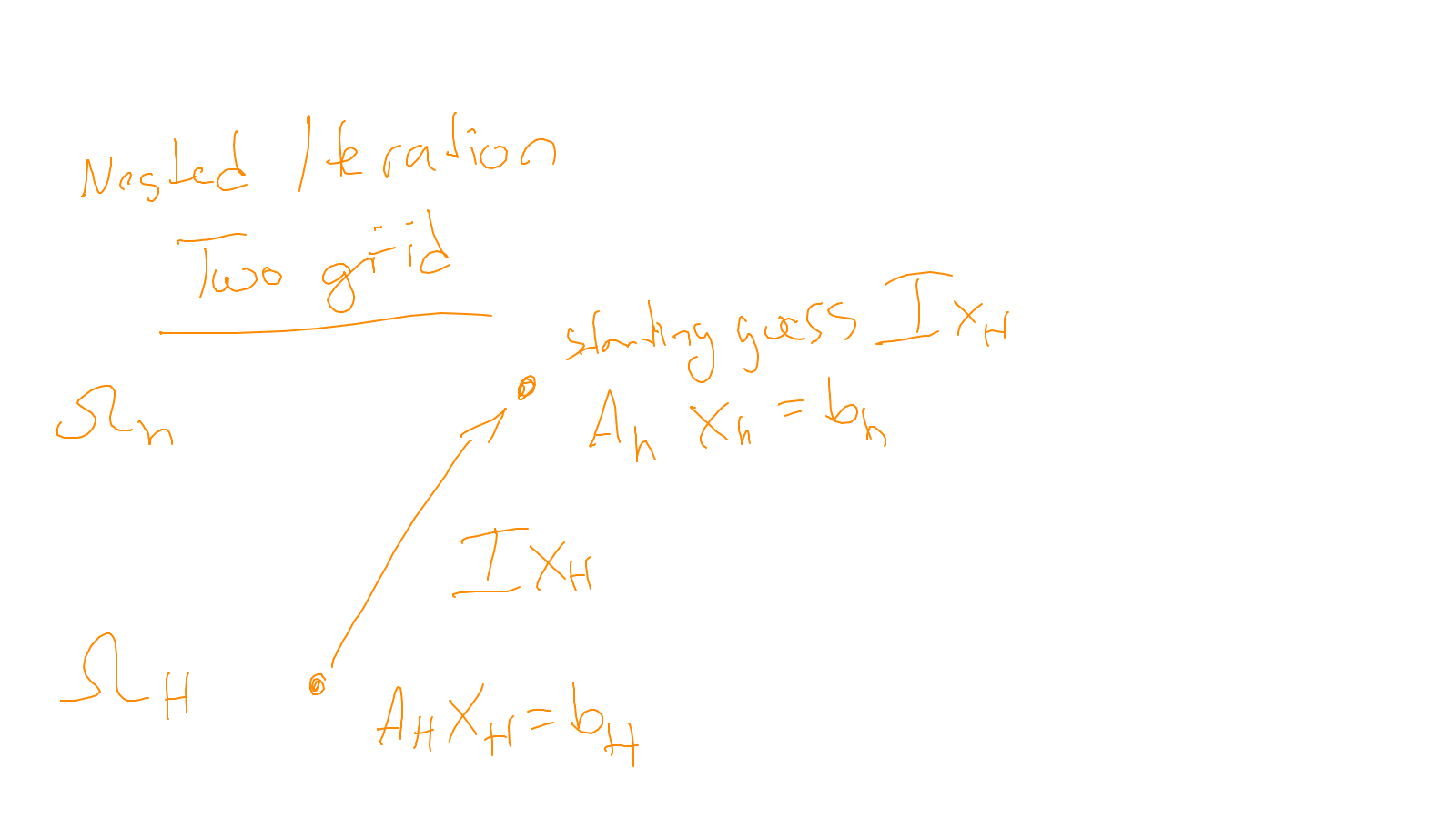
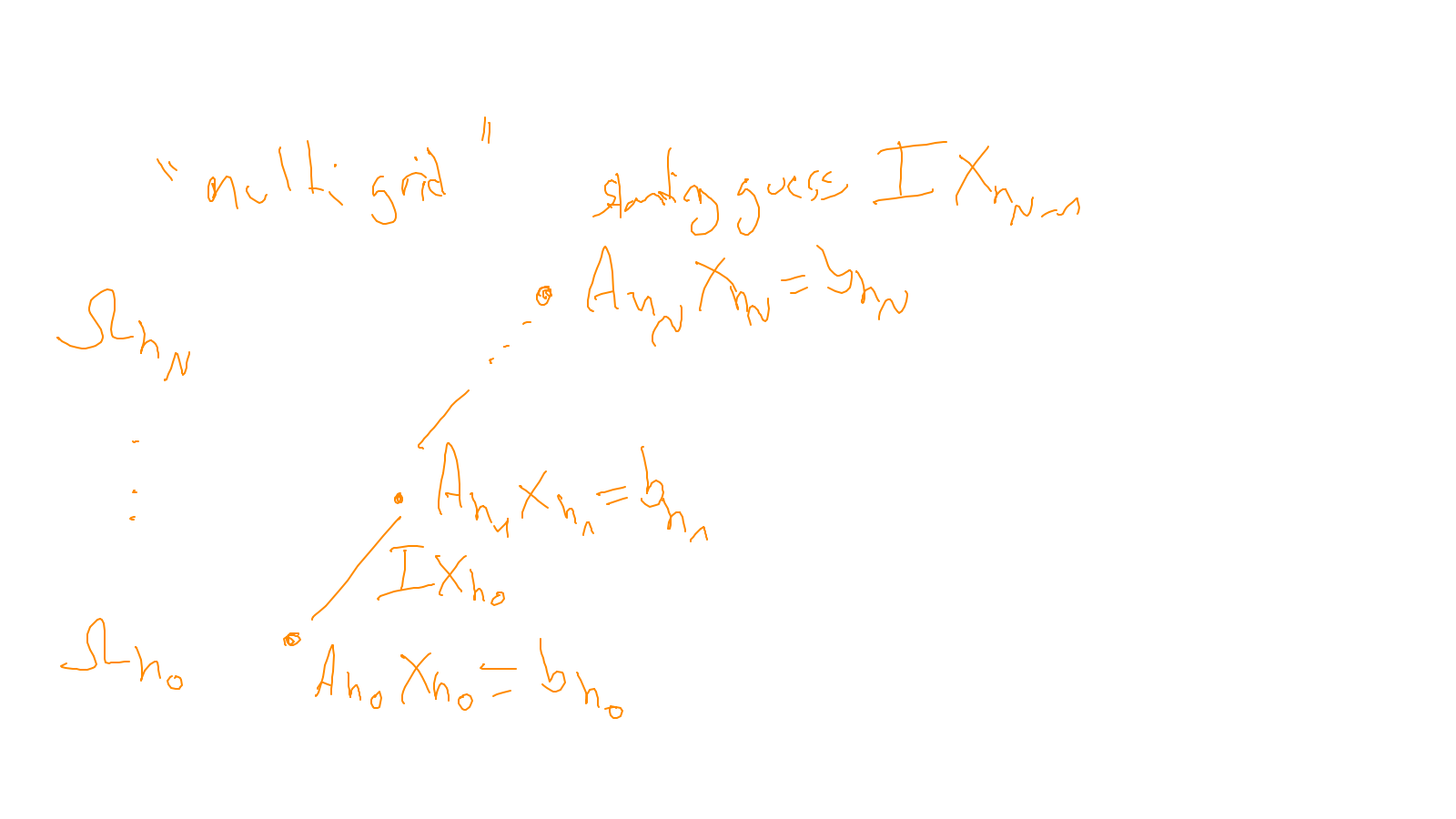
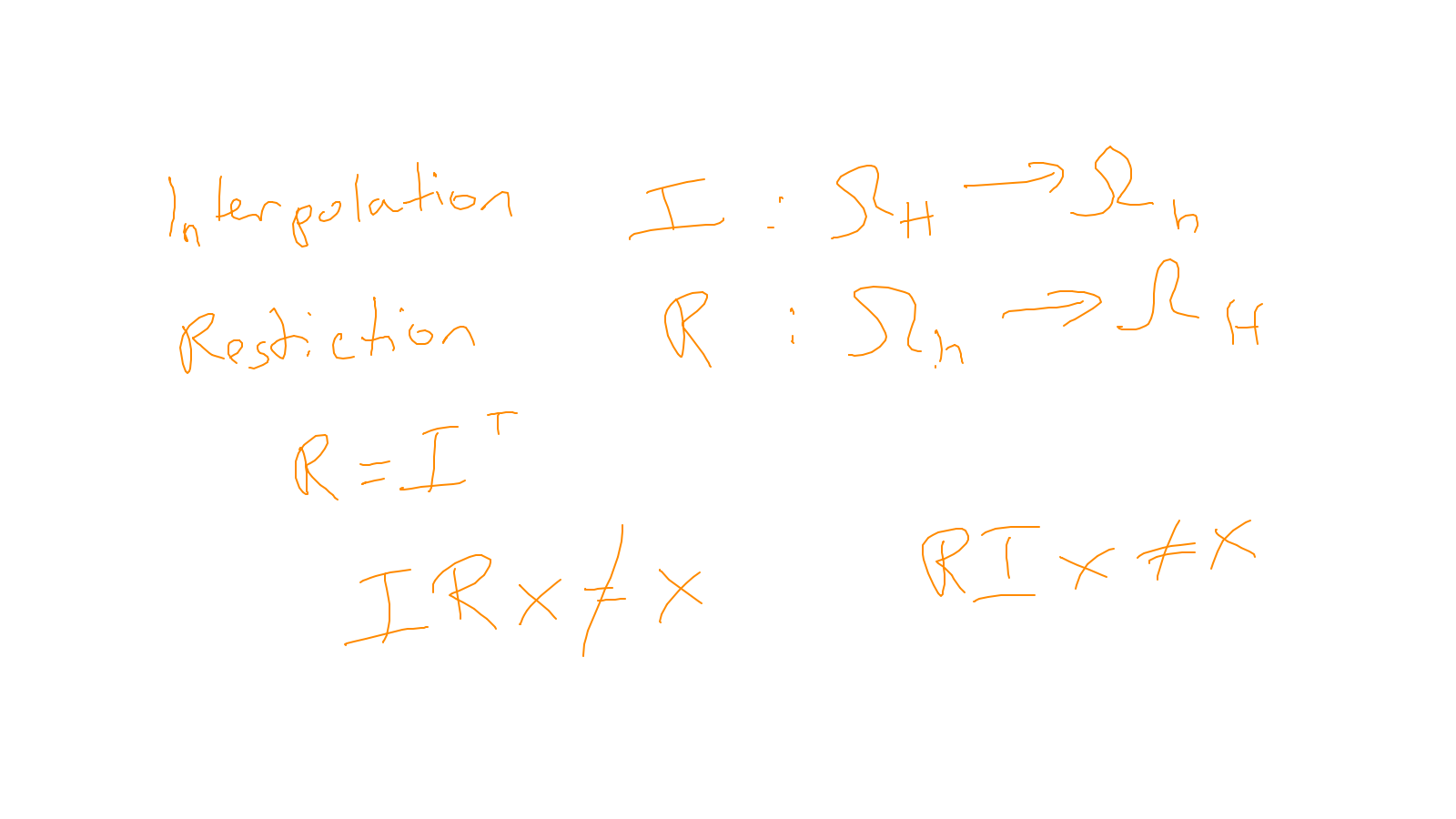
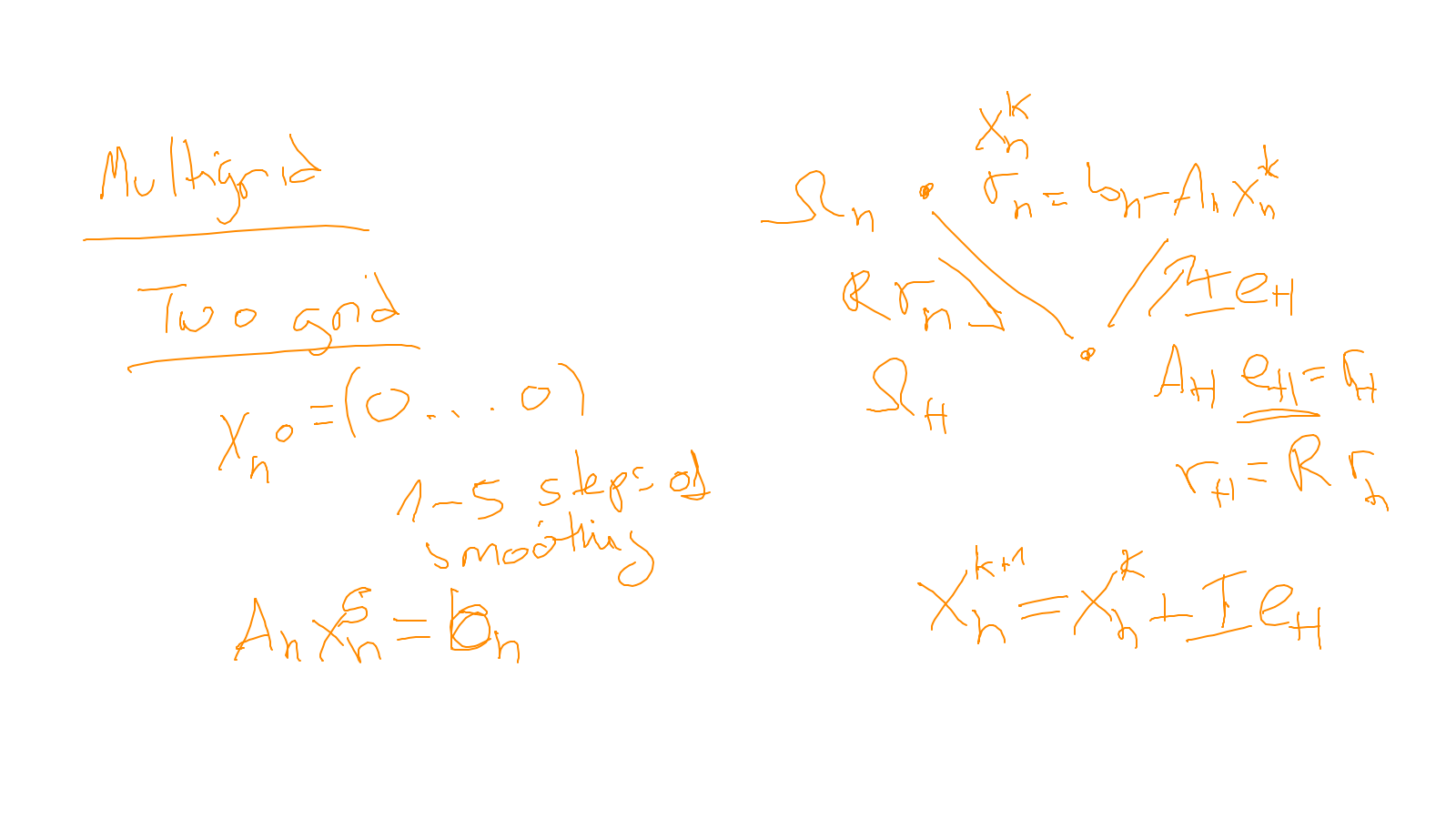
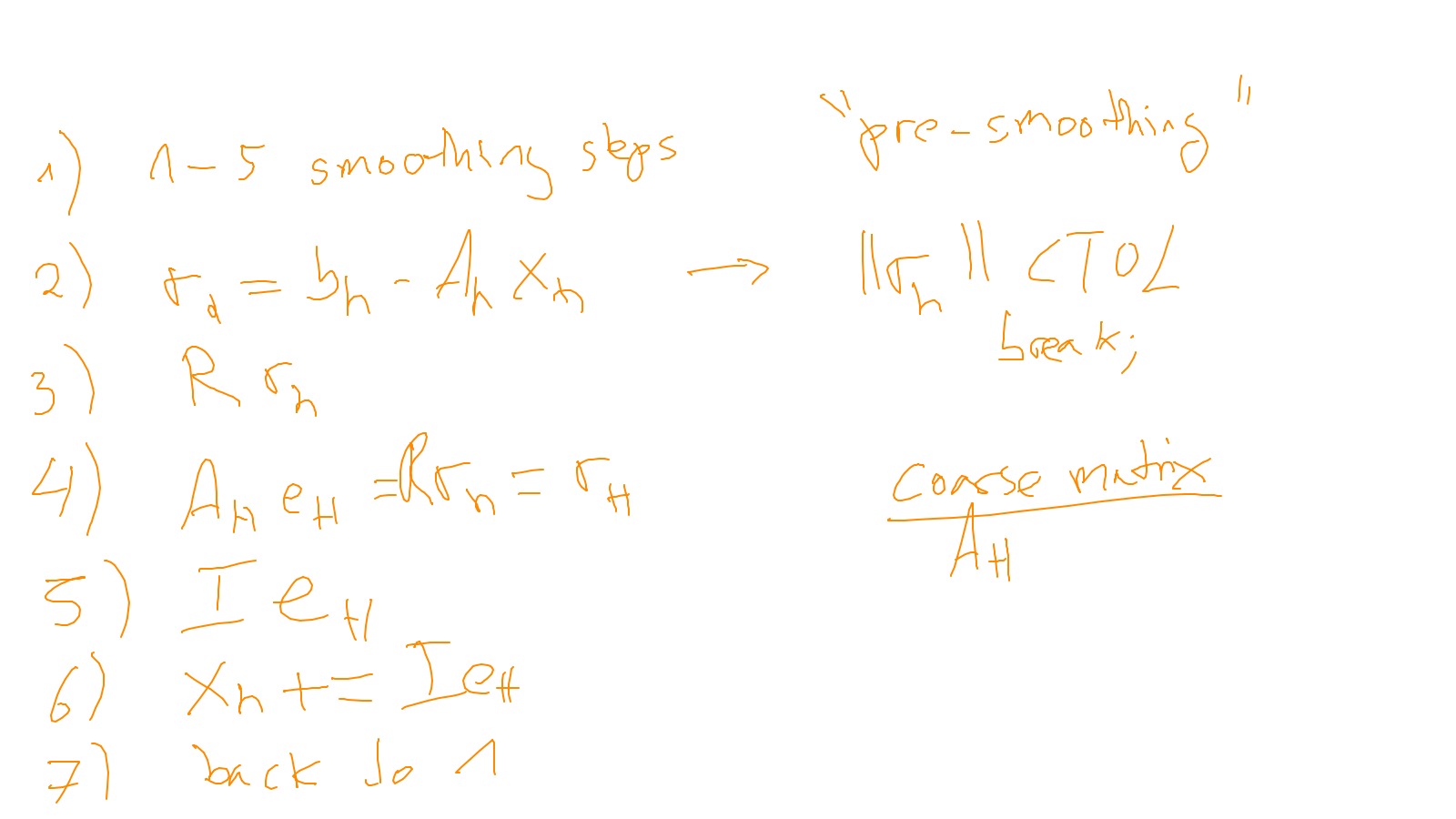
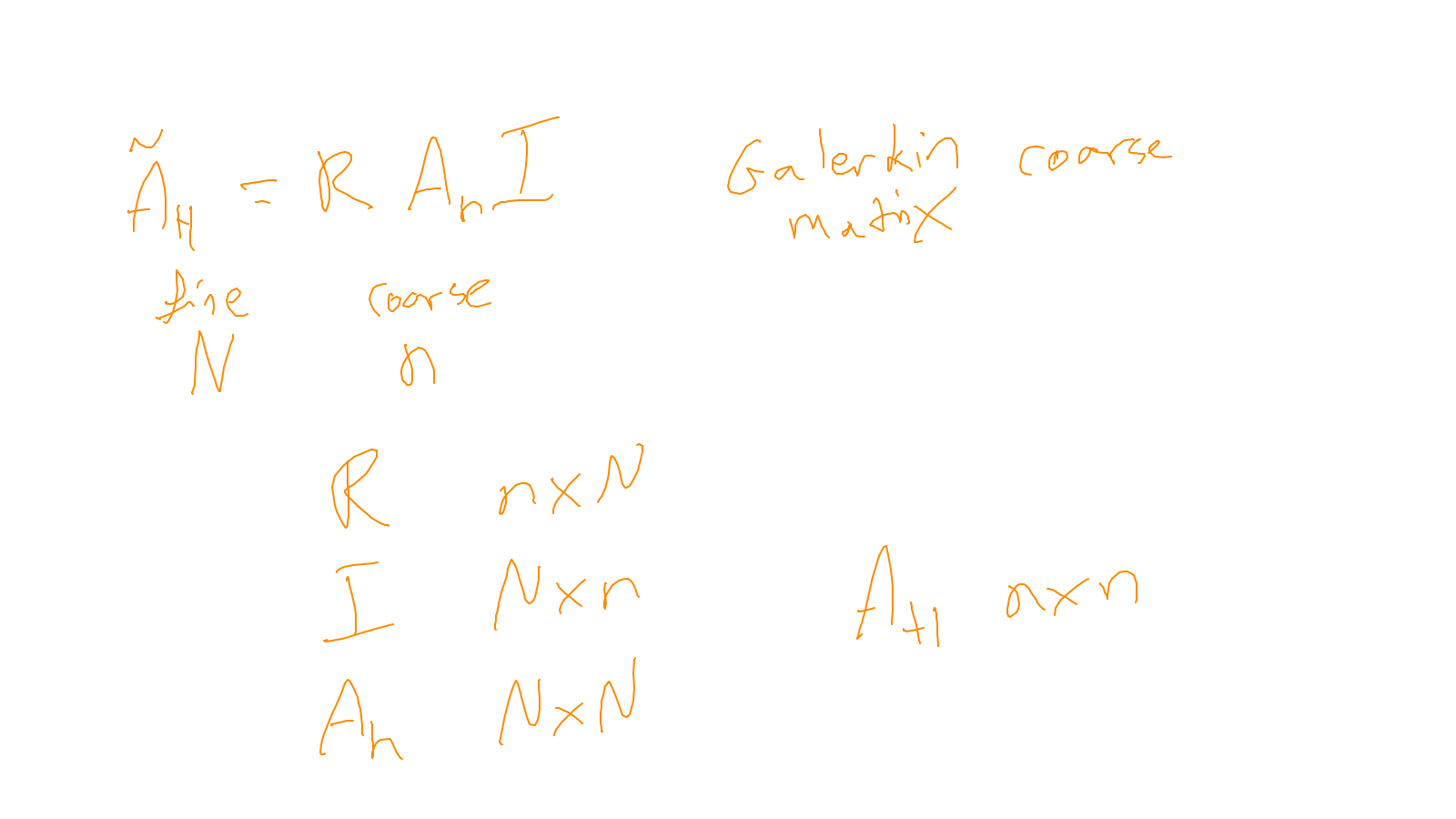
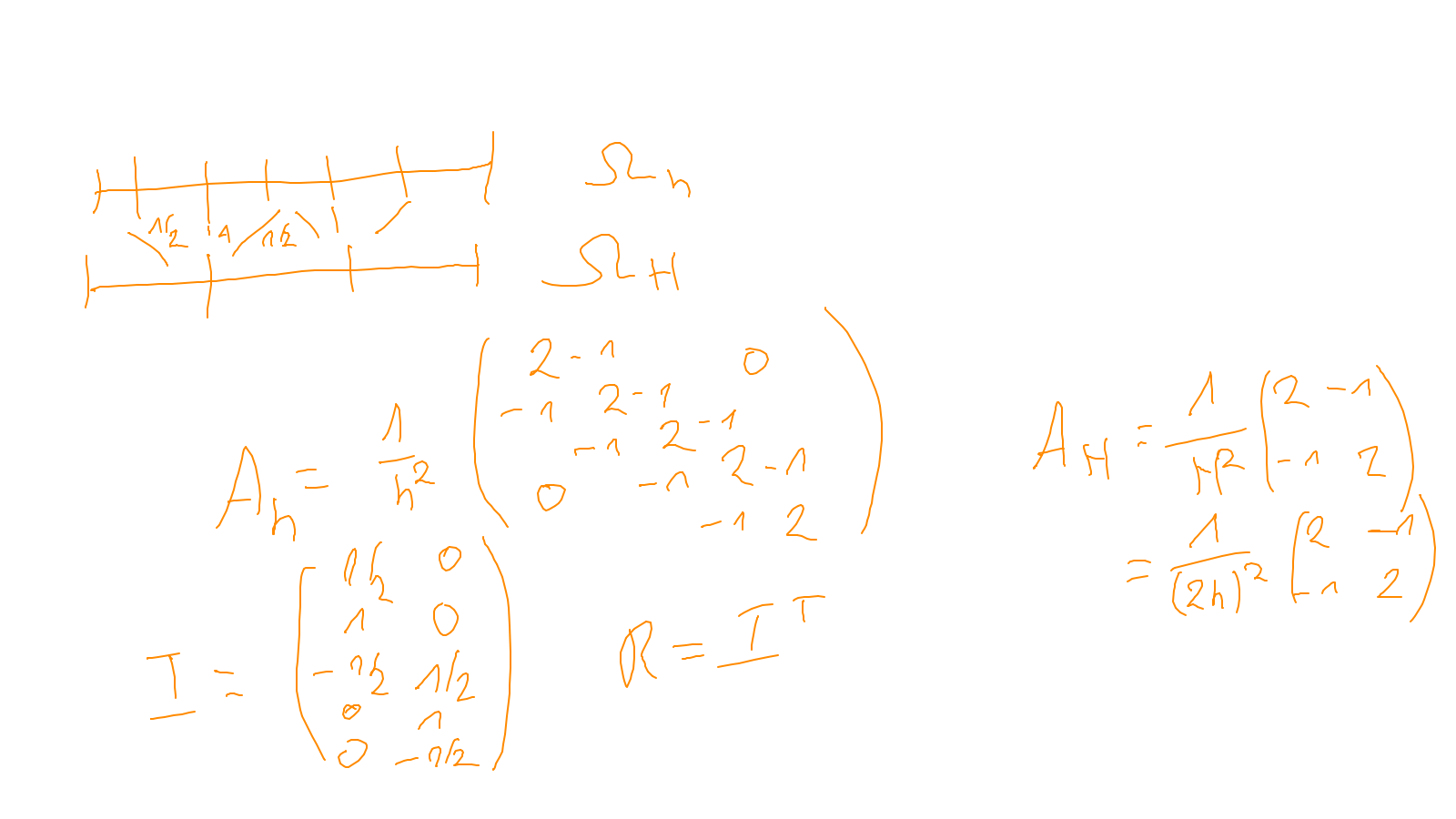
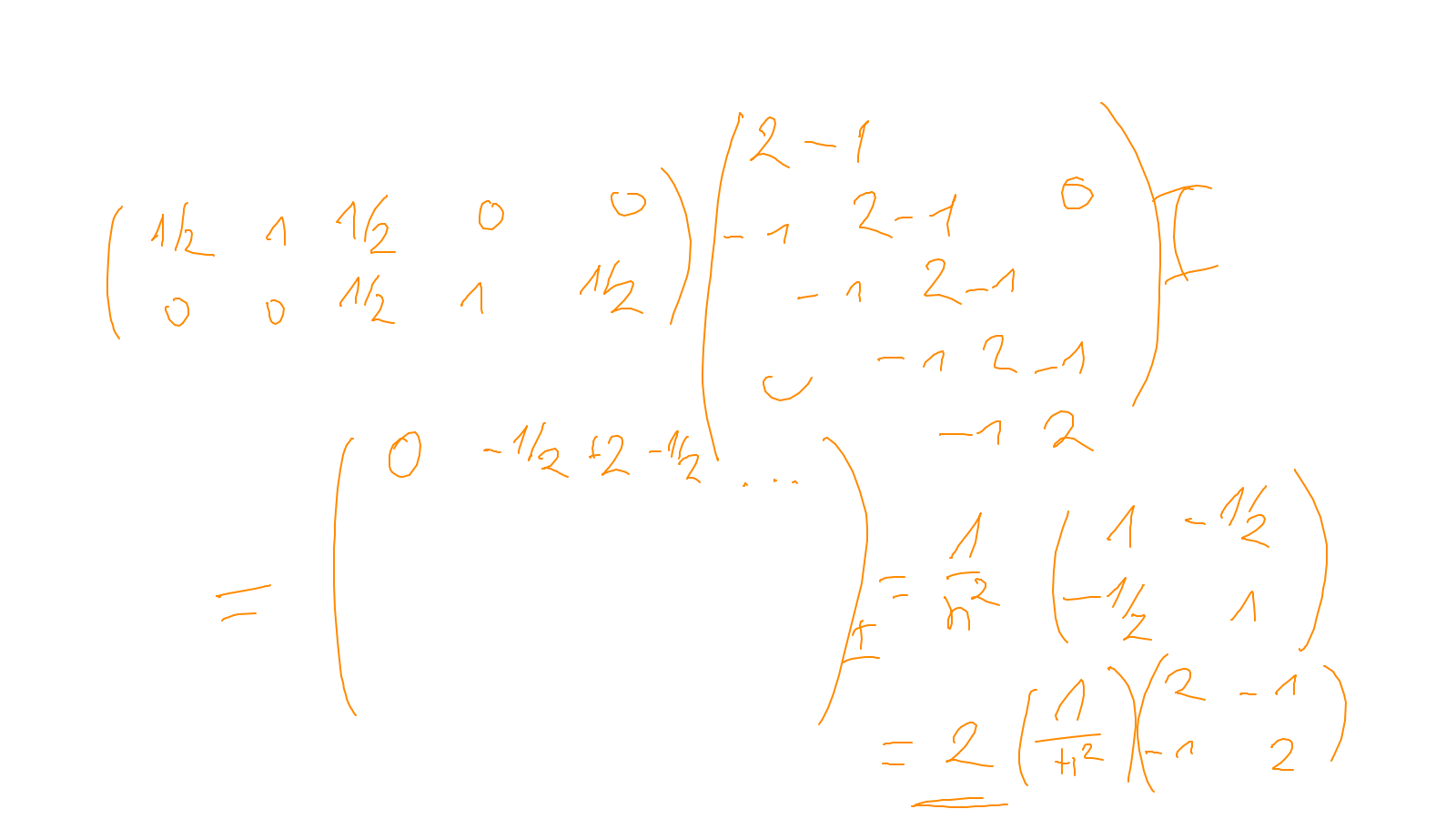
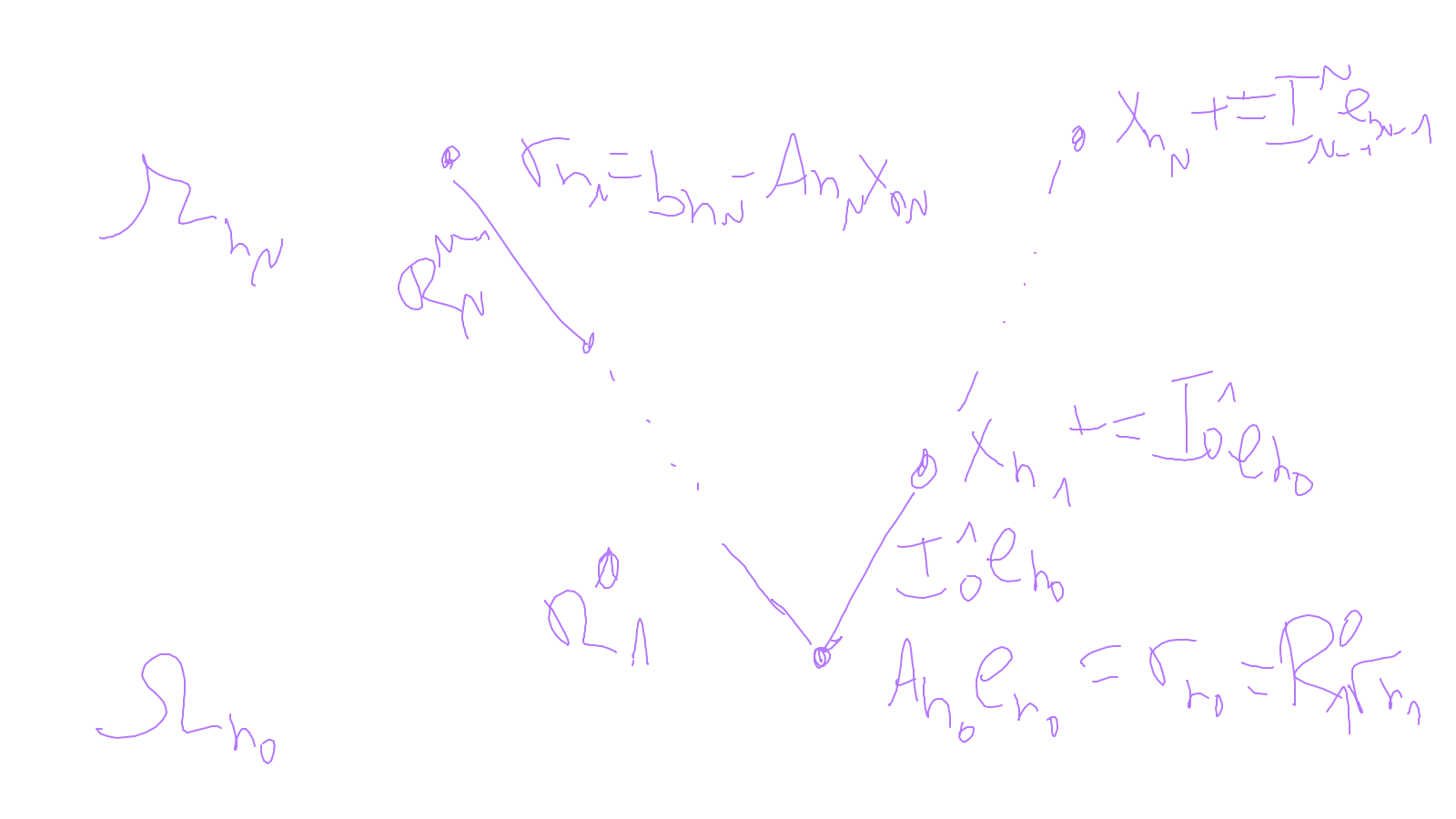
Lecture 8: timestepping #
We finish the discussion of multigrid method: ipython notebook
We will begin looking at time-stepping methods (for now in an ODE setting): ipython notebook
The video is now available at: video
The content of the whiteboard can be found below. It is also all contained in the ipython notebook itself.
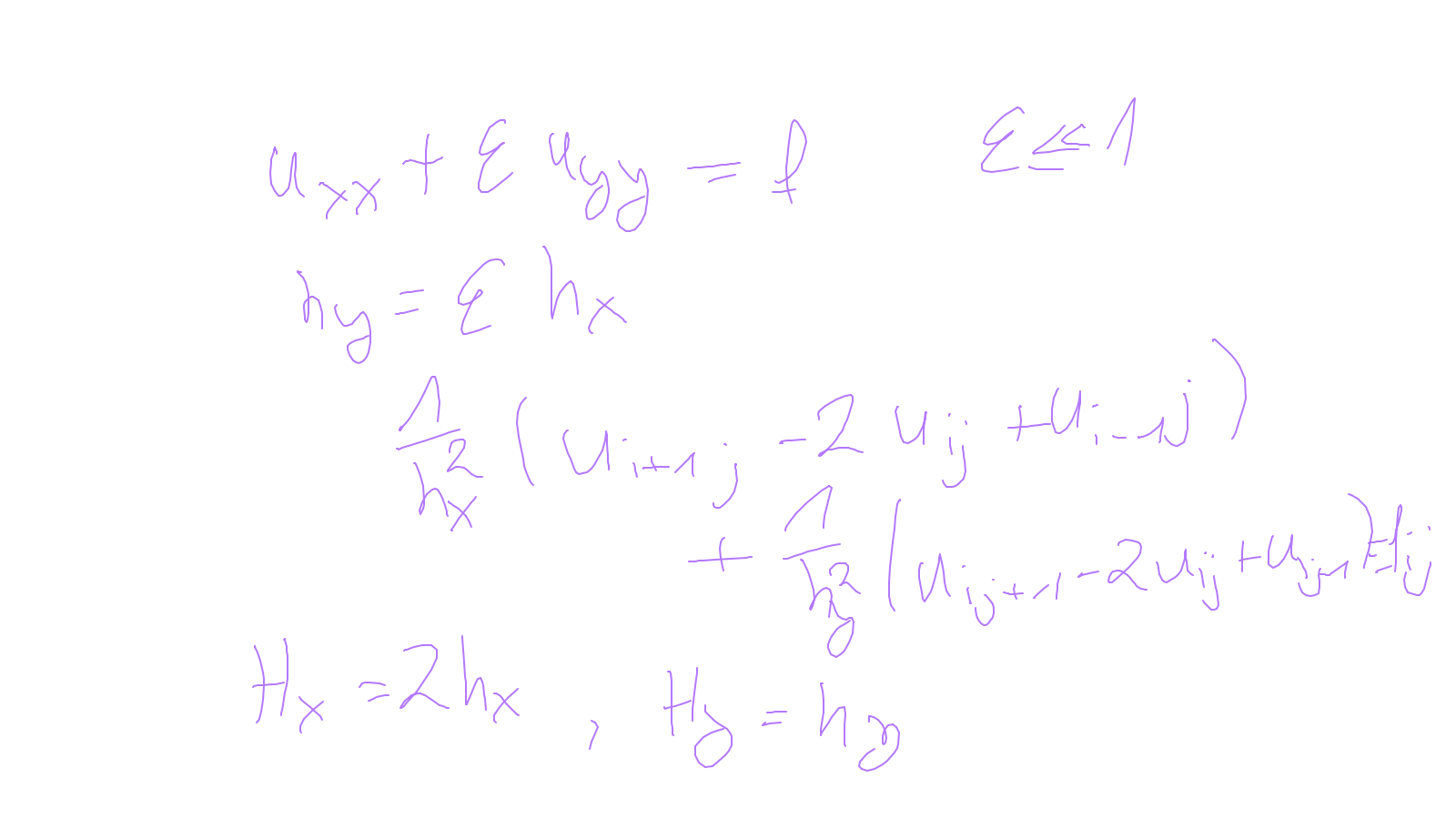
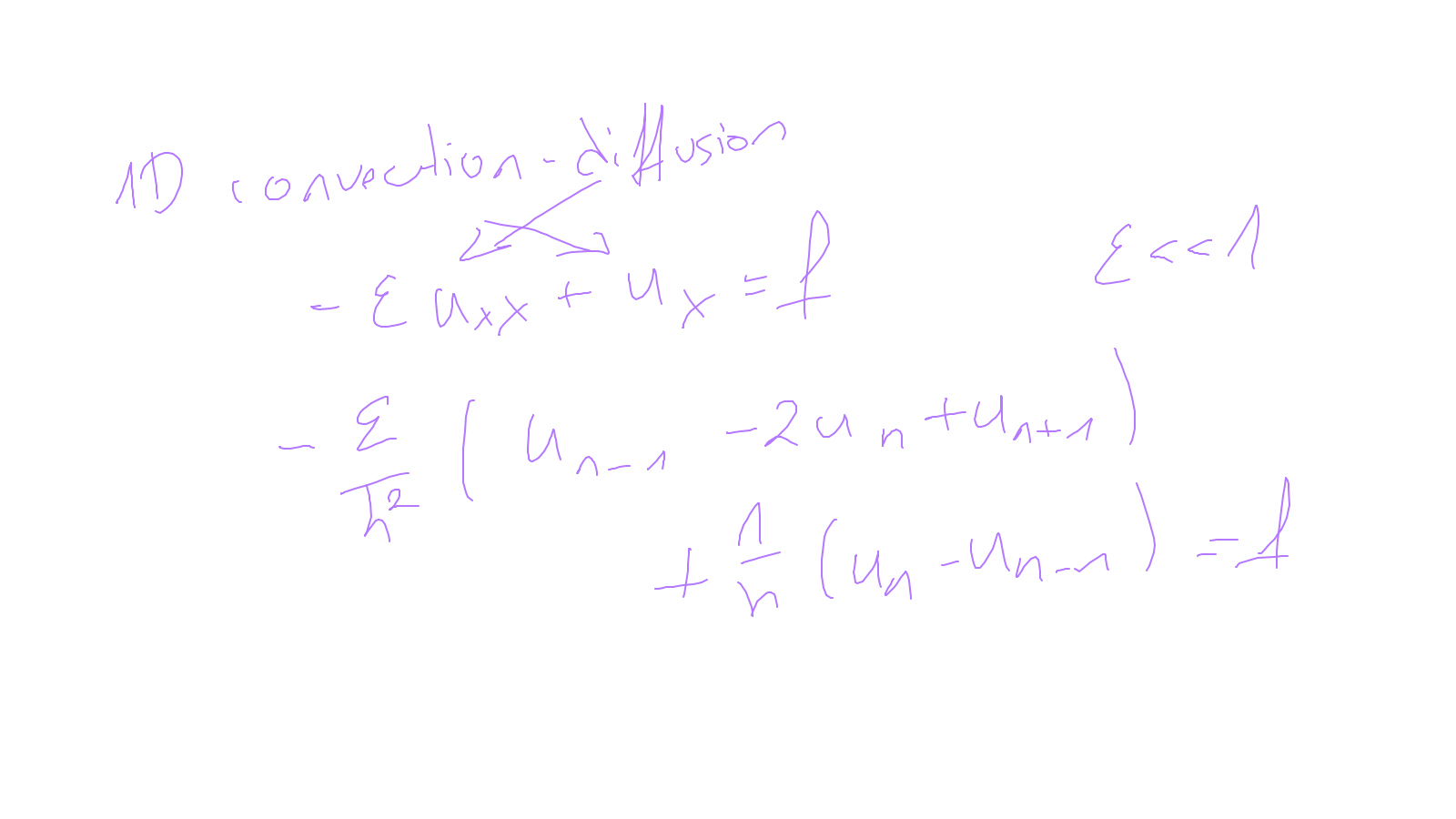
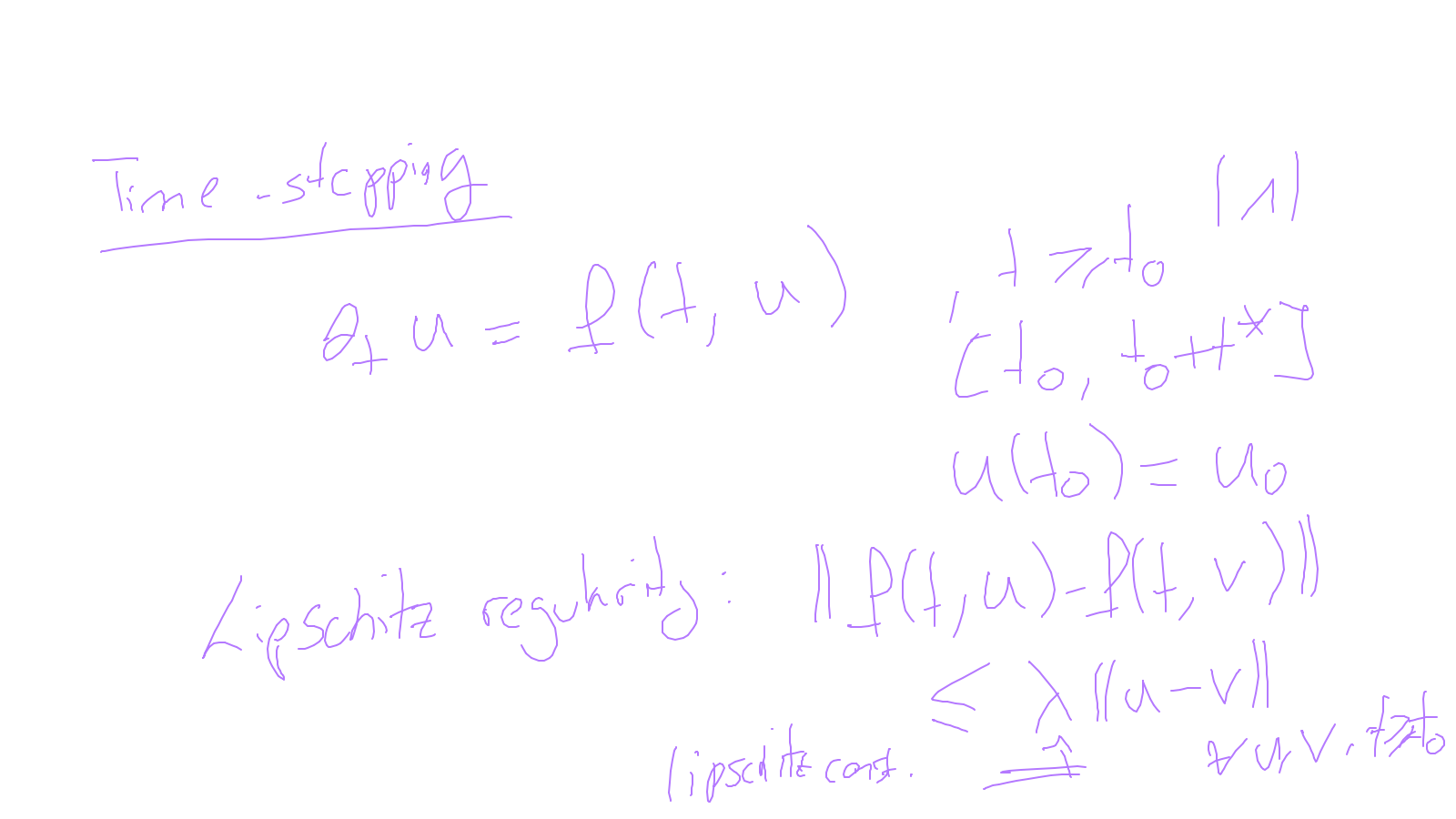
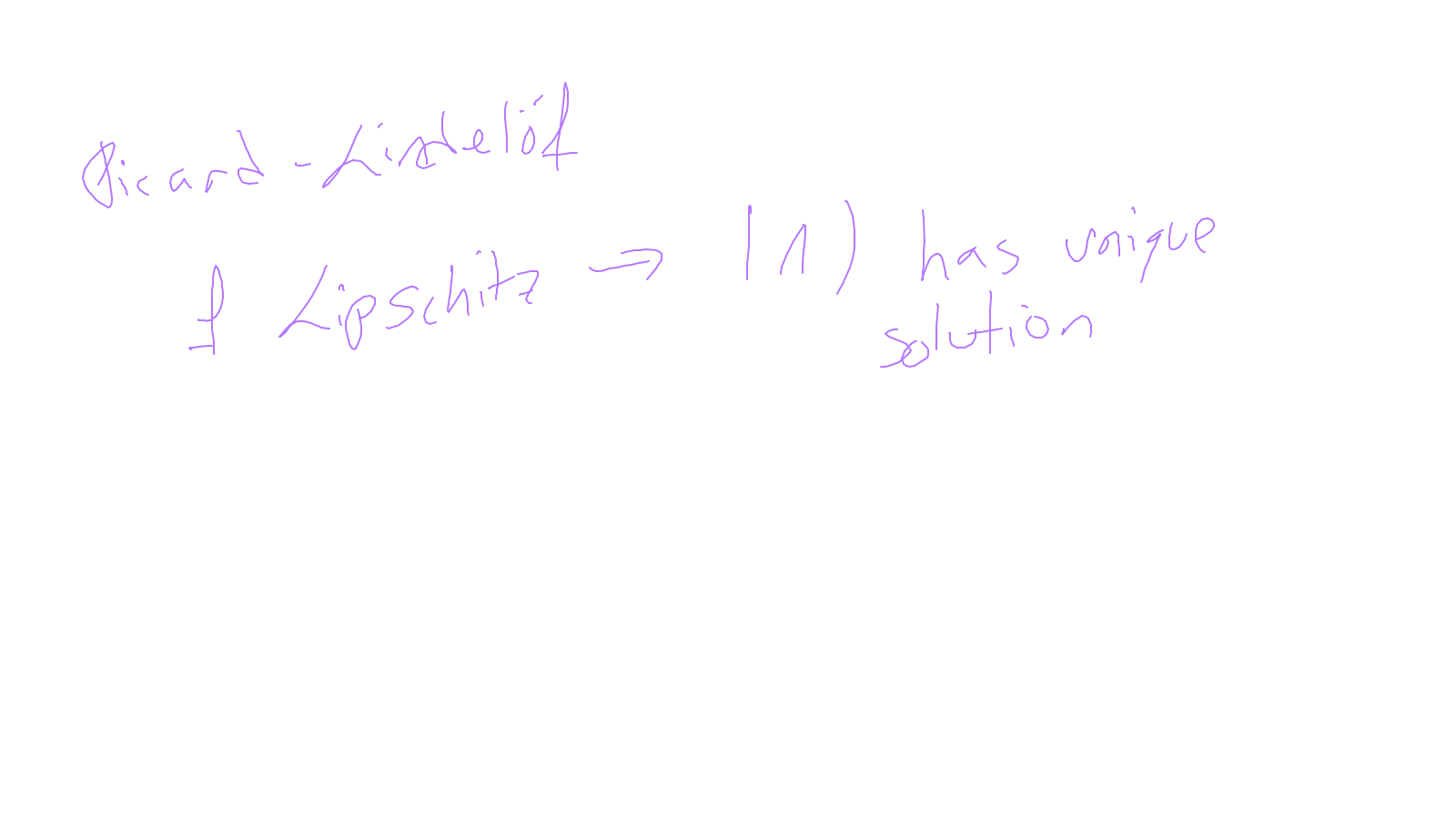
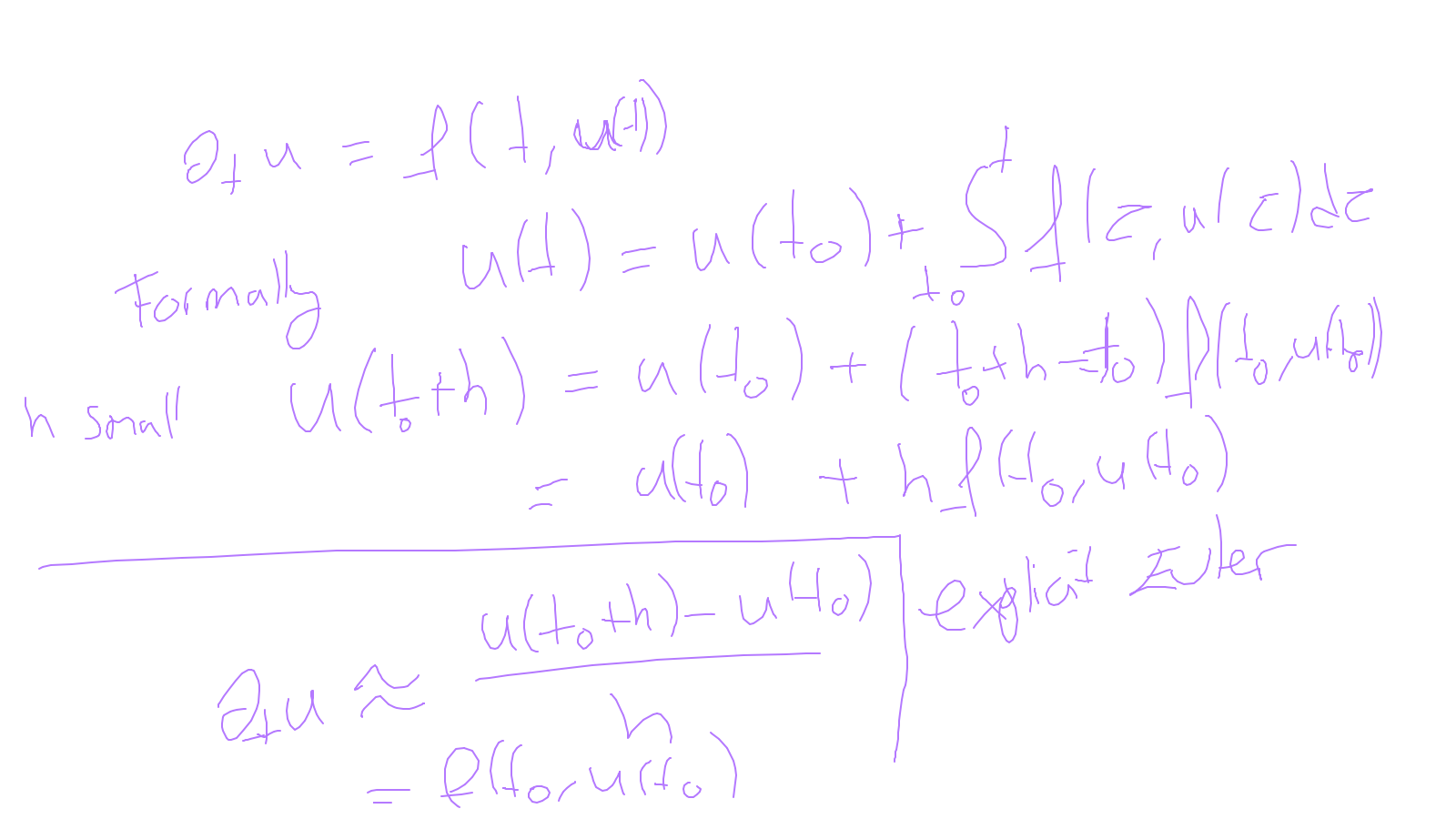
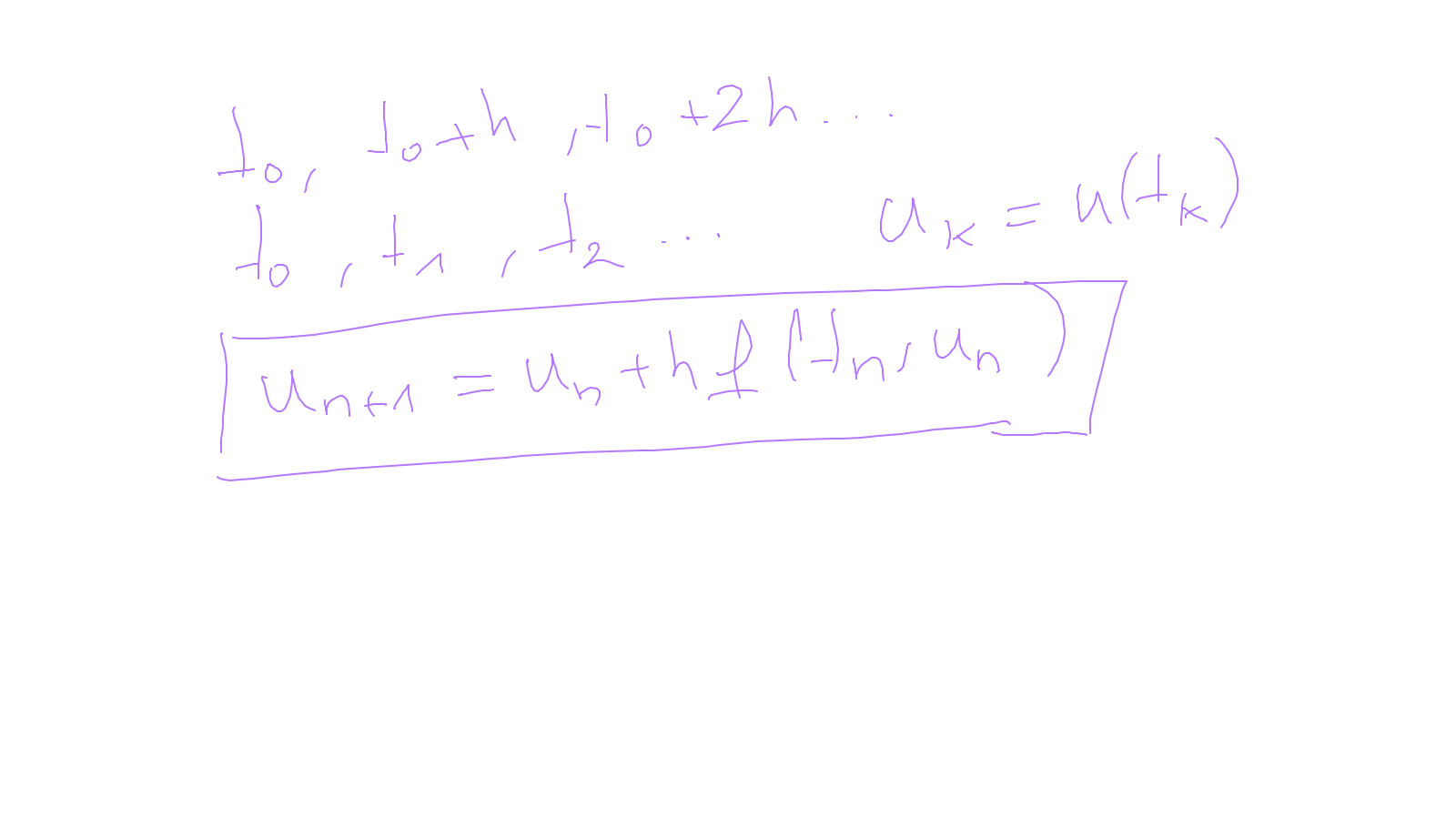
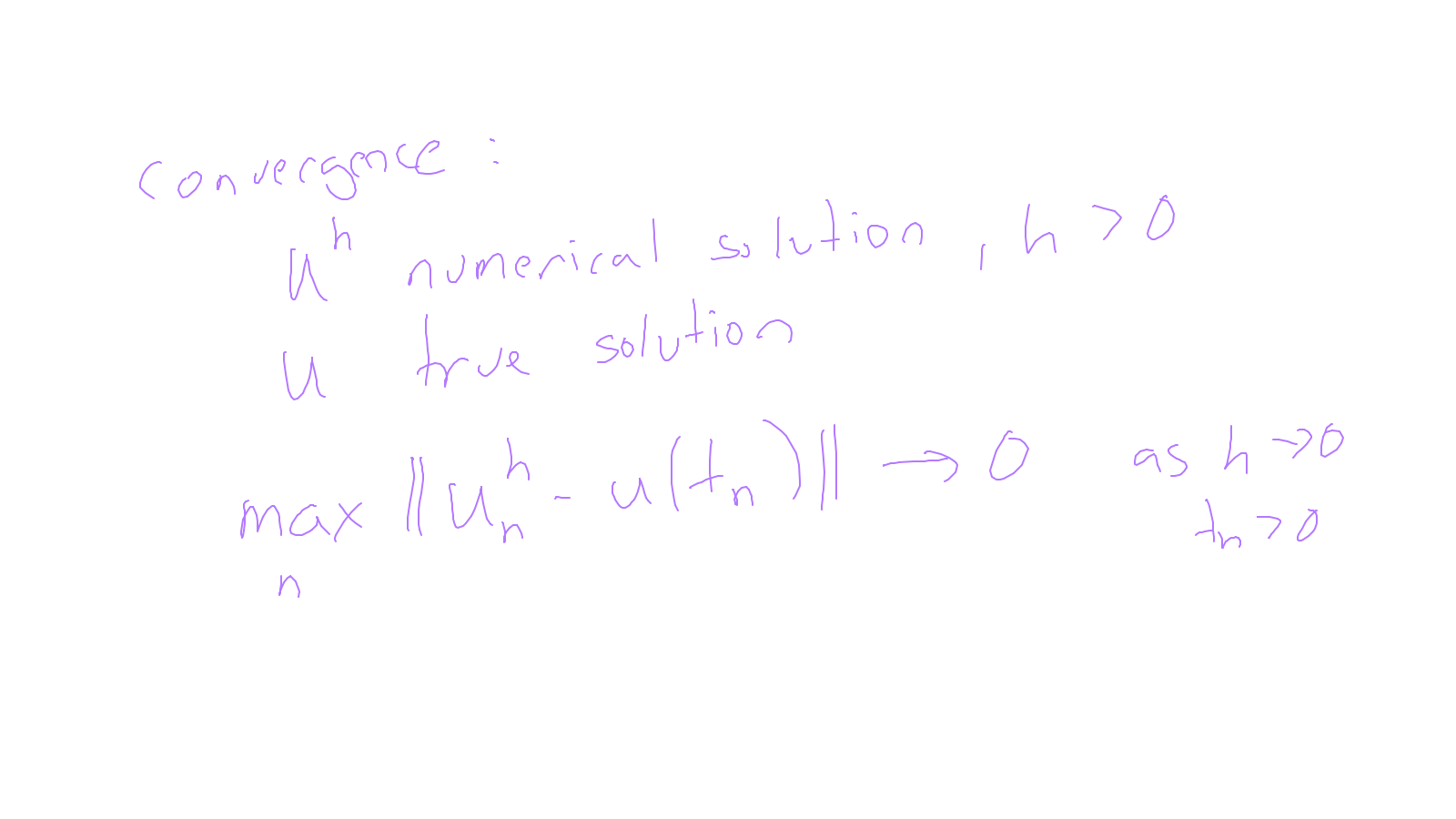
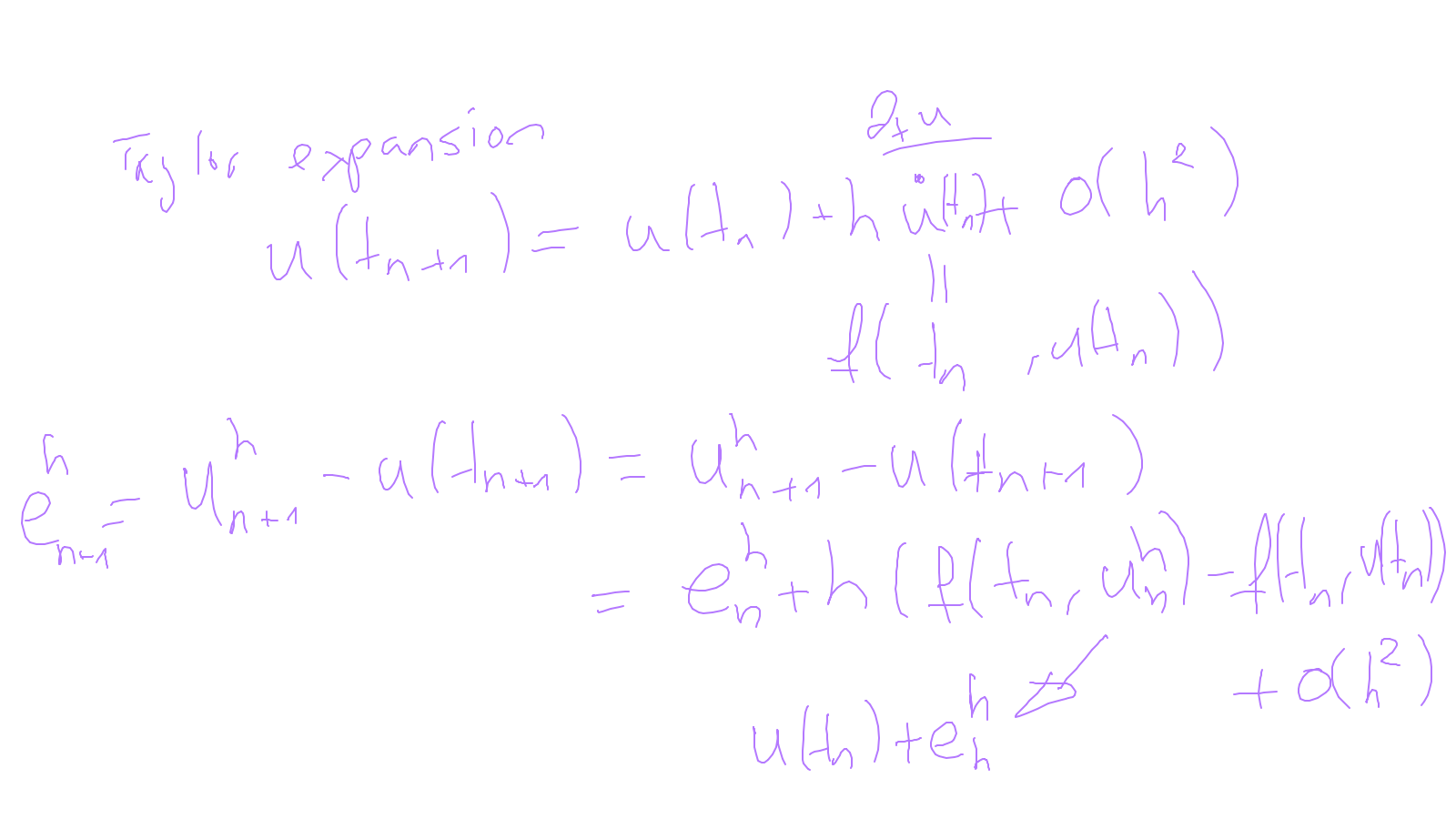
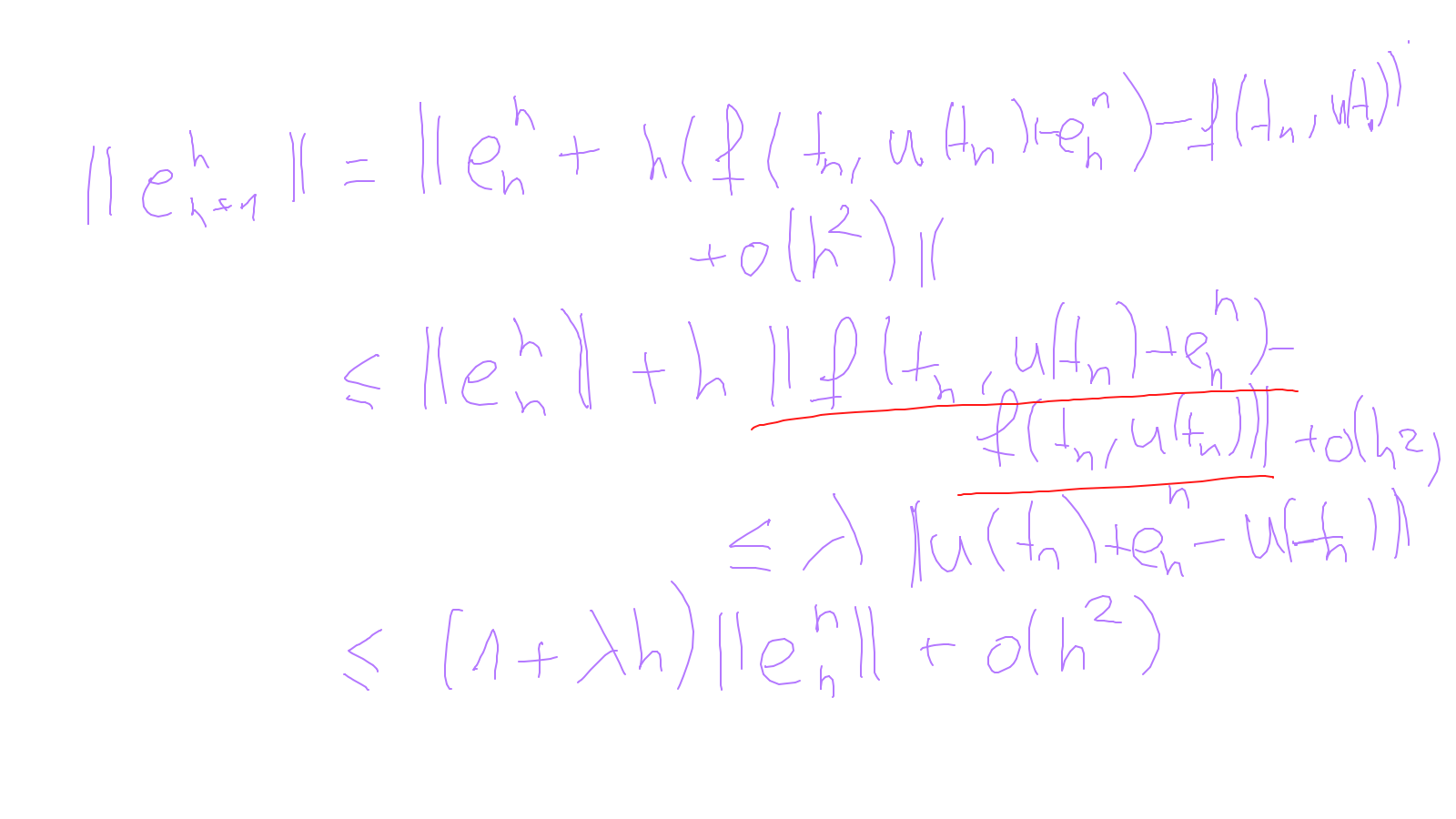
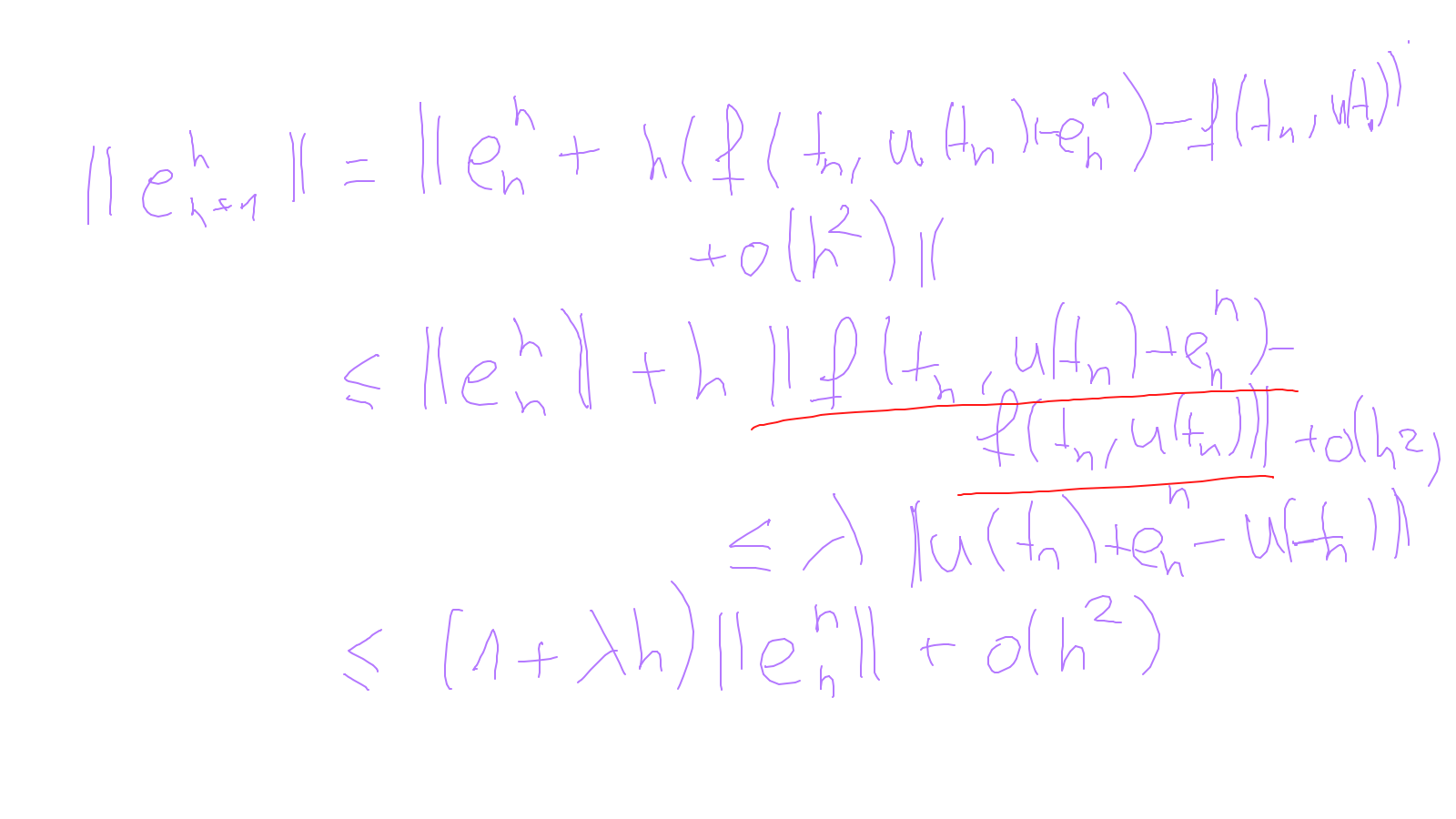

Lecture 9: time-stepping #
We will finish time-stepping methods (for now in an ODE setting): ipython notebook and: ipython notebook.
Please go through the high-order part of the notebook on your own.
The video is now available at: video
The content of the whiteboard can be found below. It is also all contained in the ipython notebook itself.
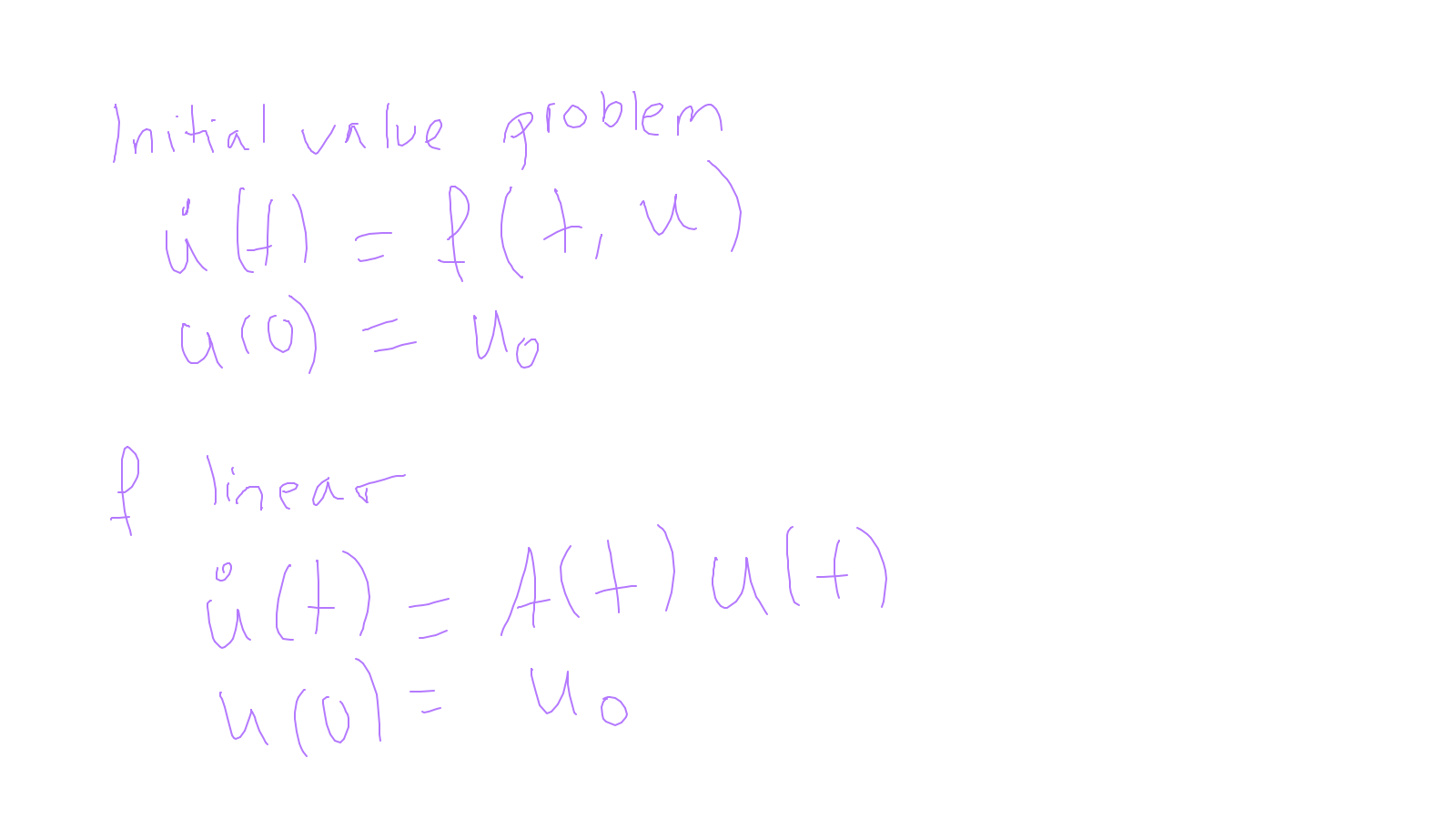
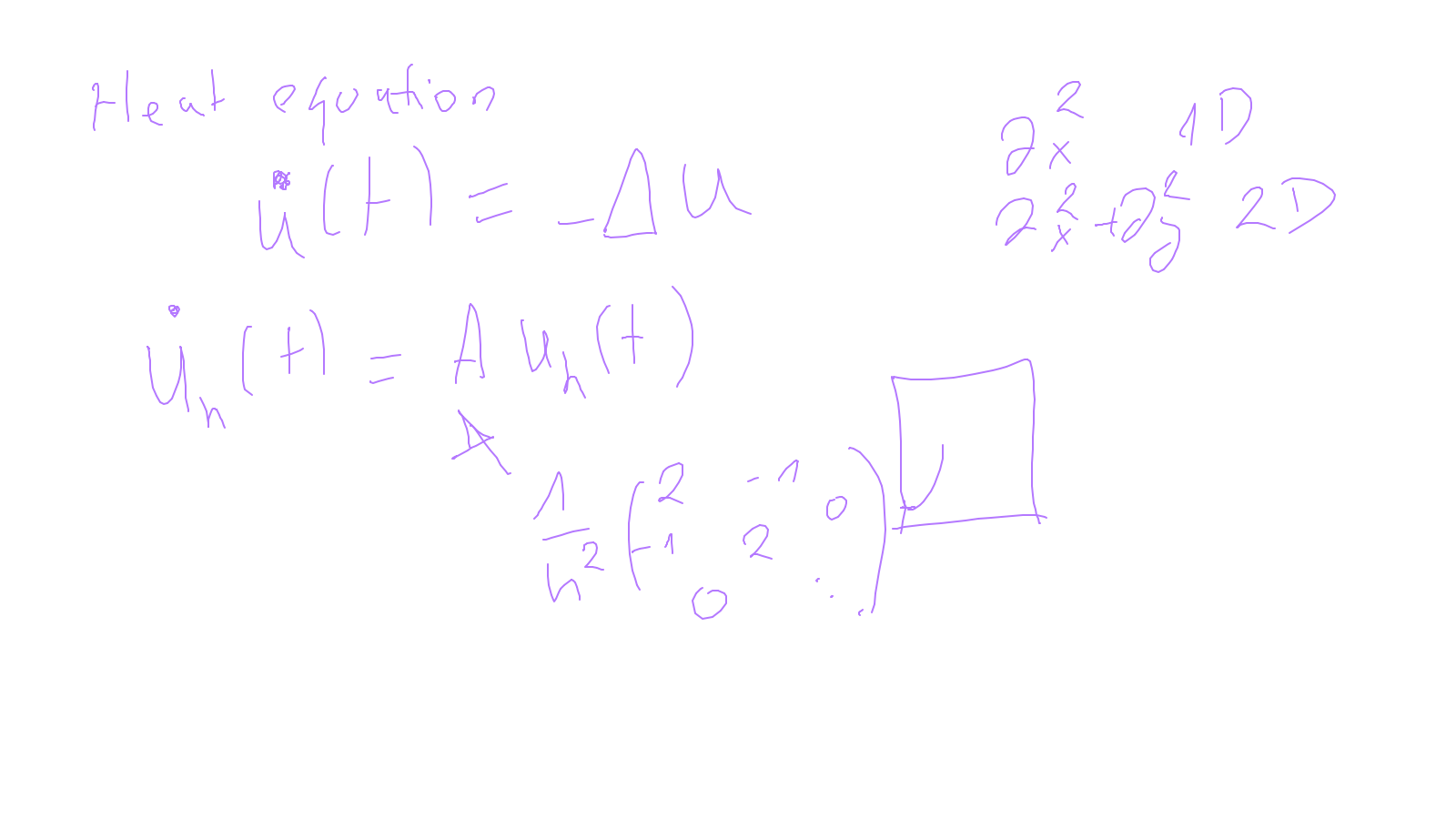
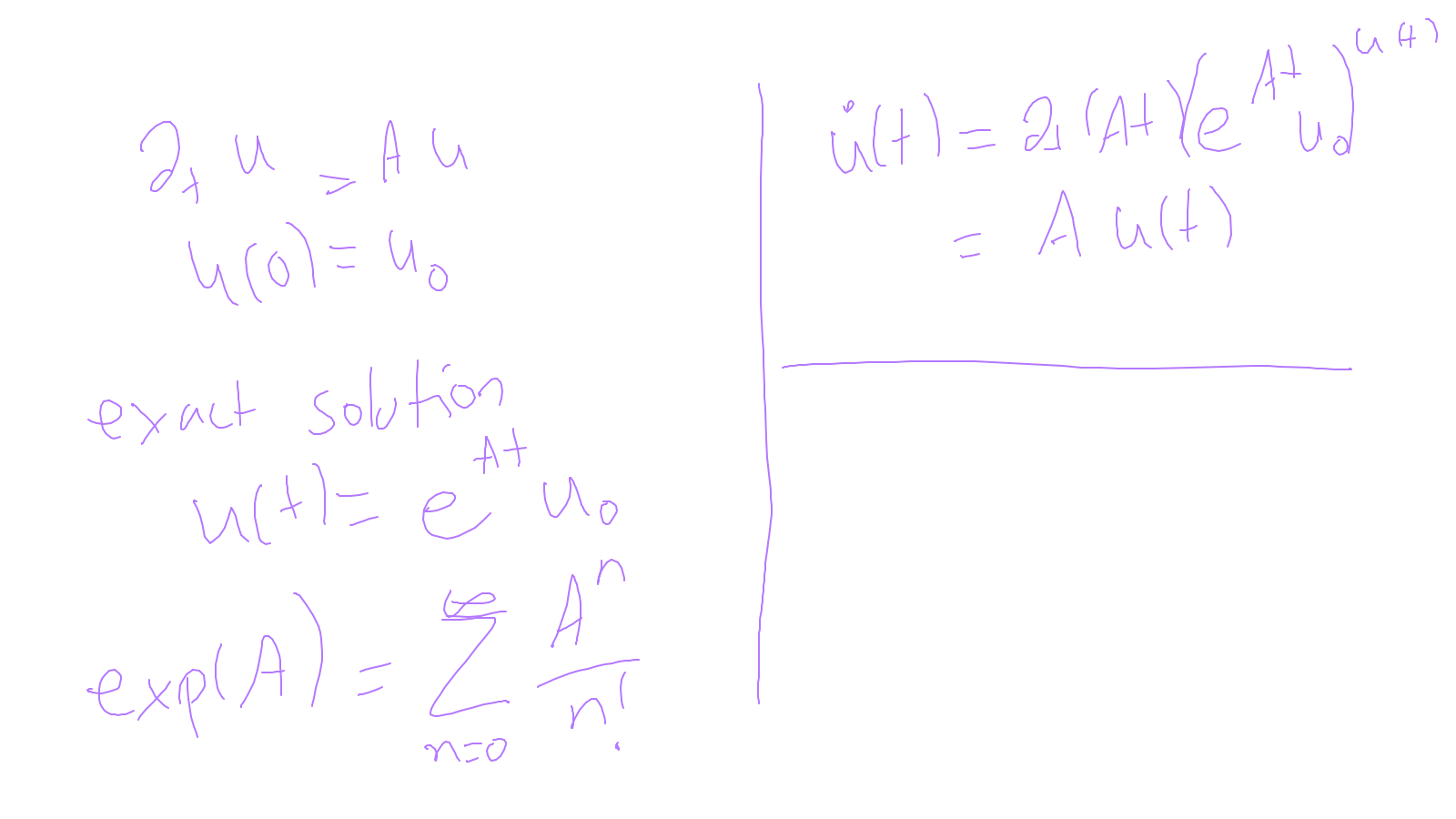
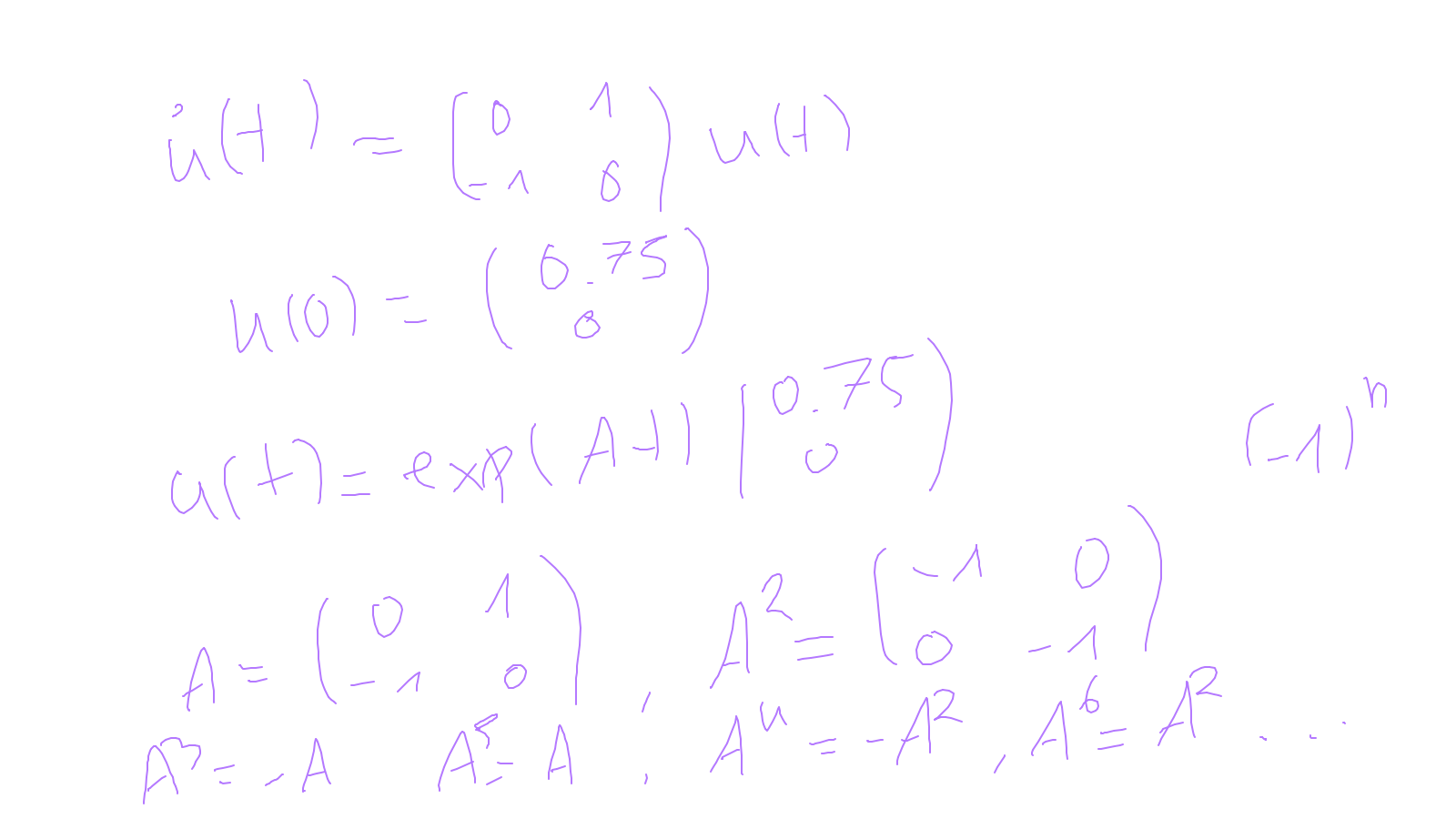
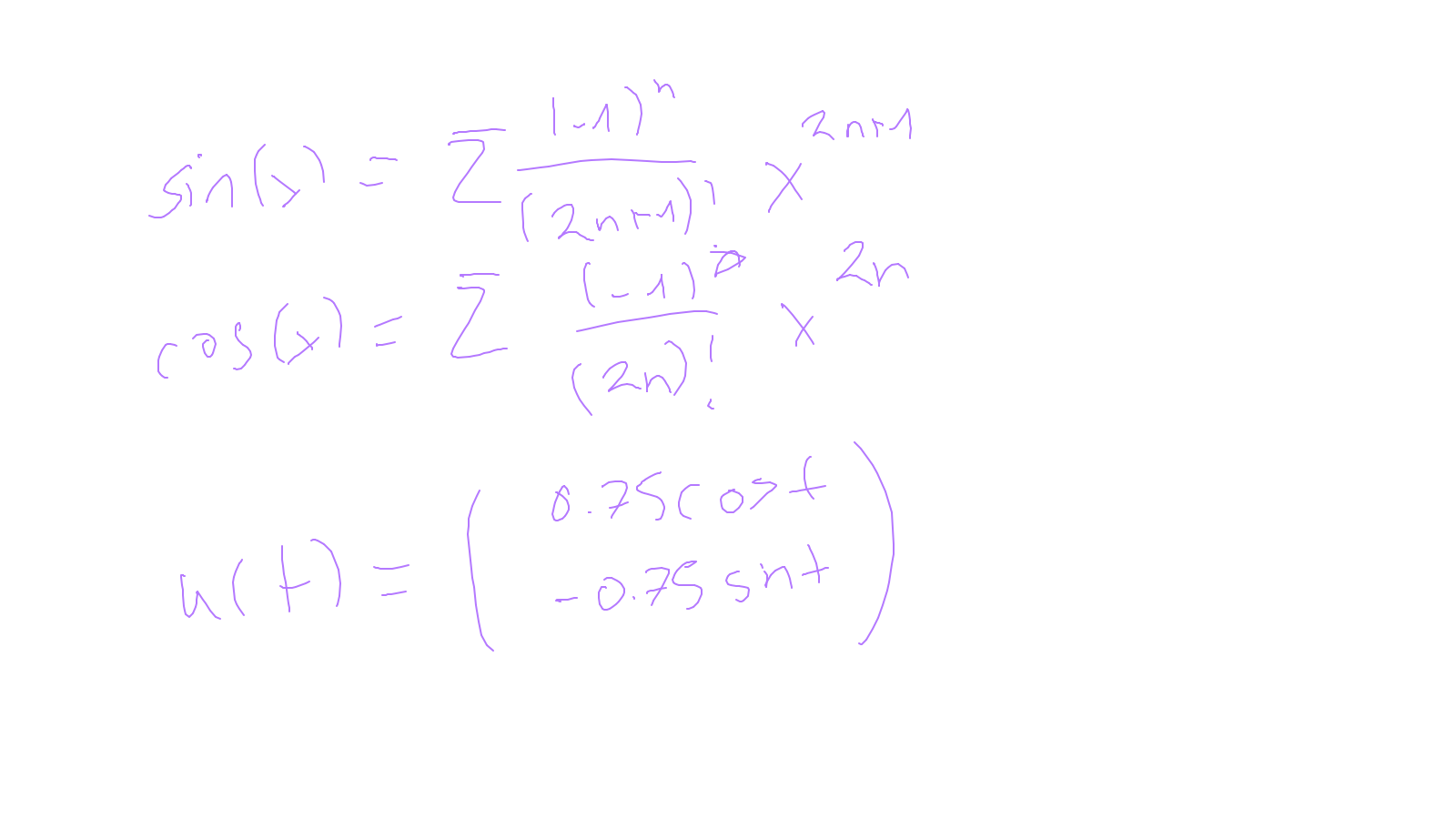
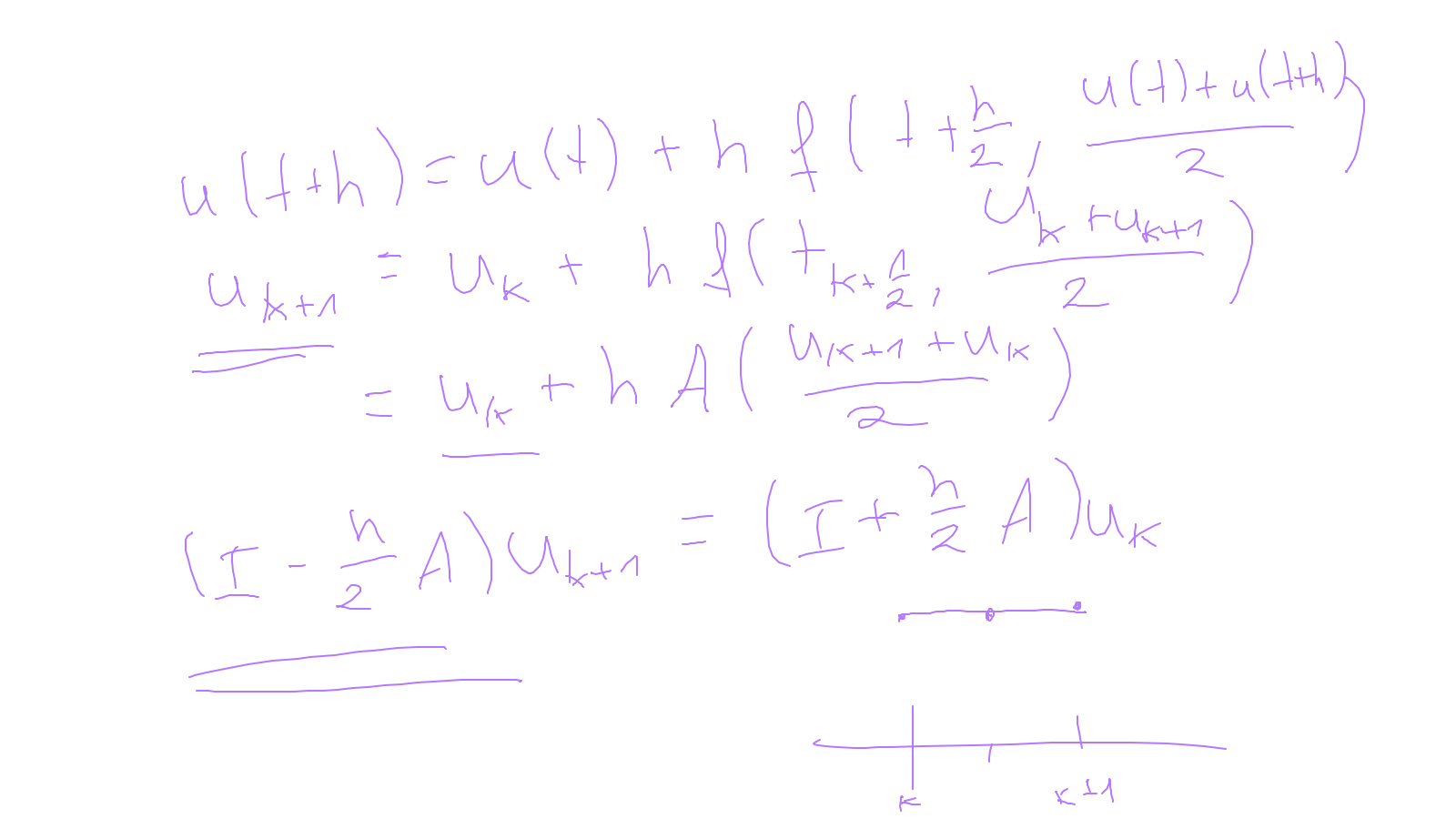
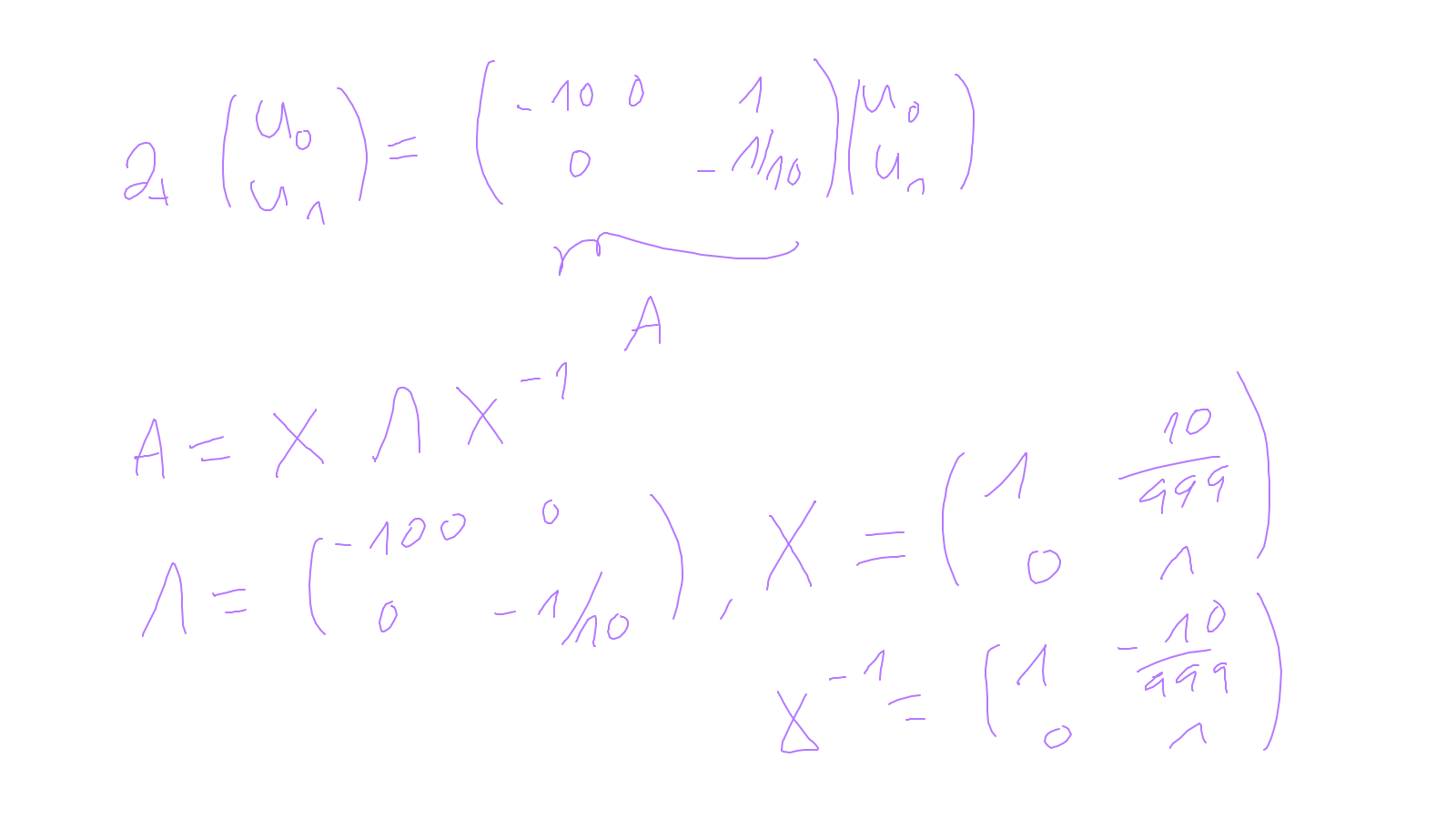
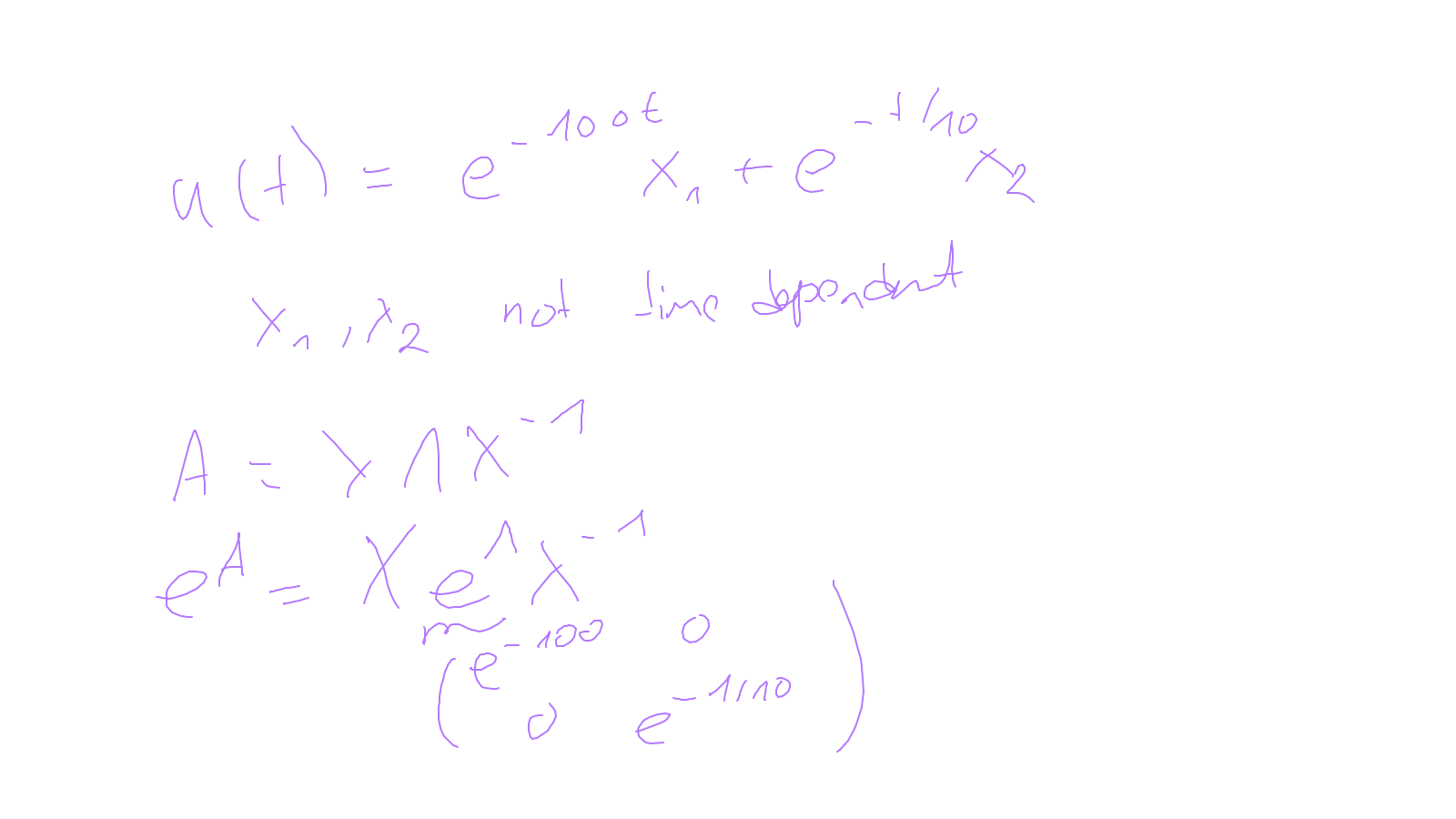
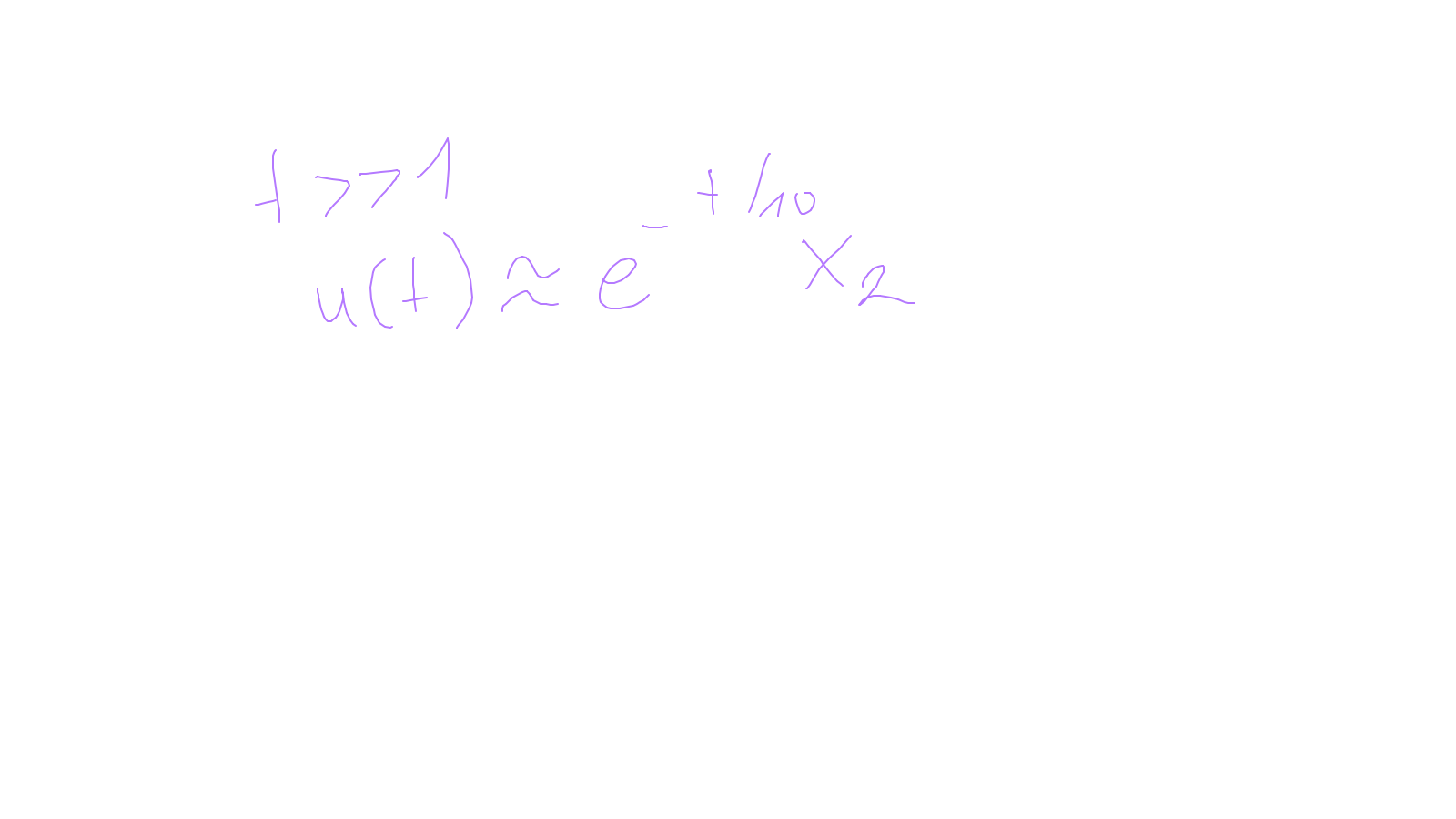

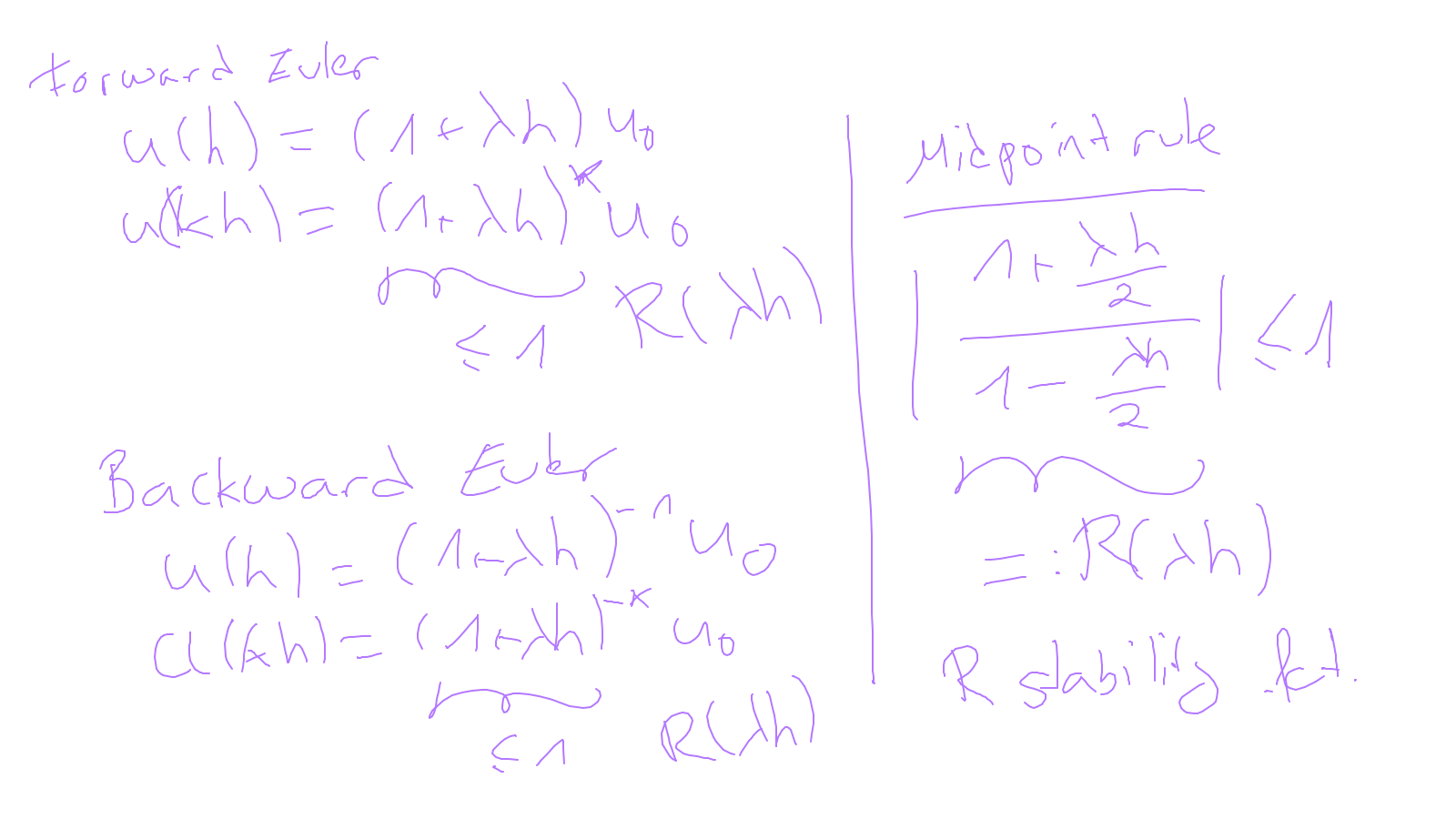
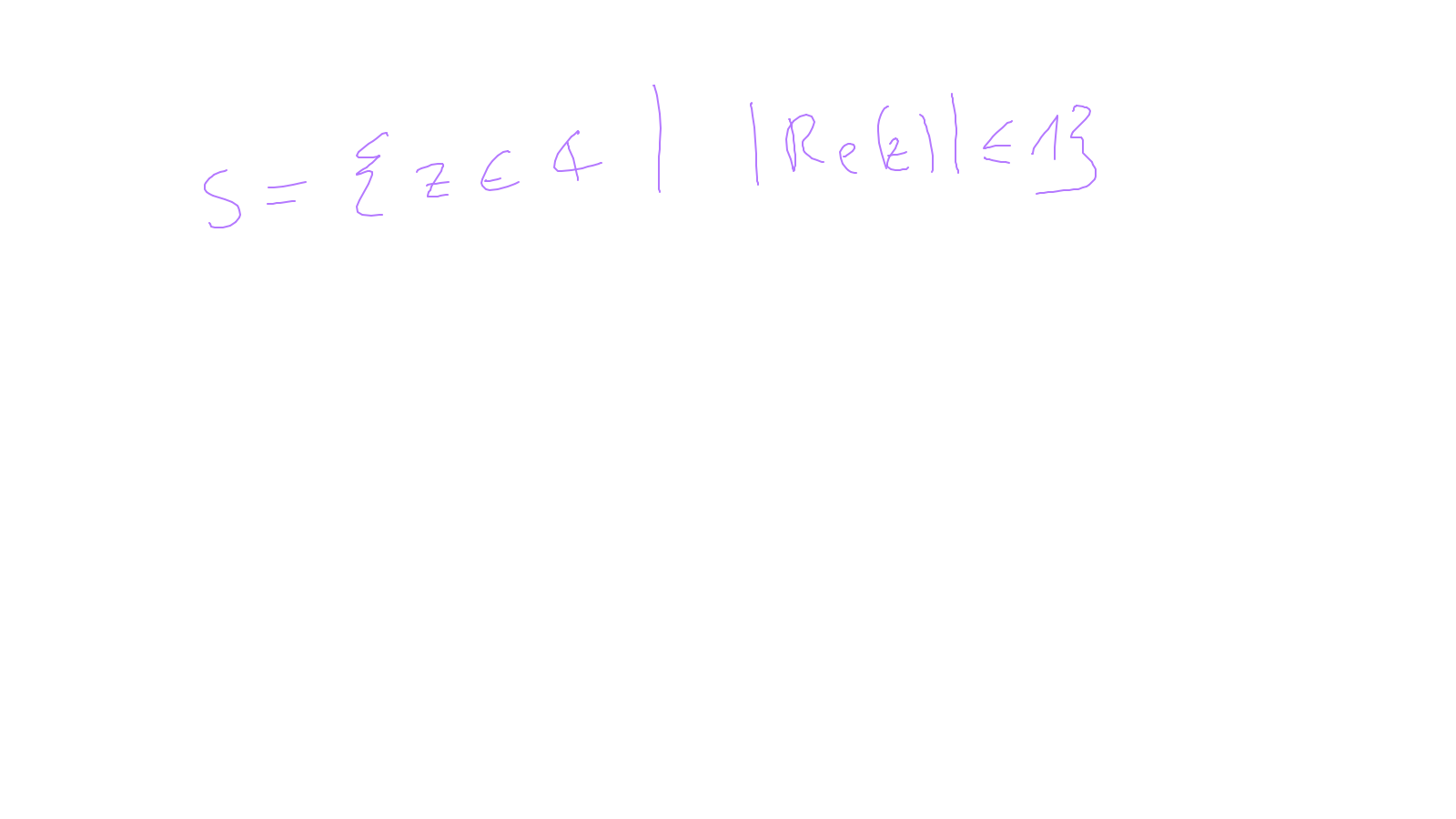
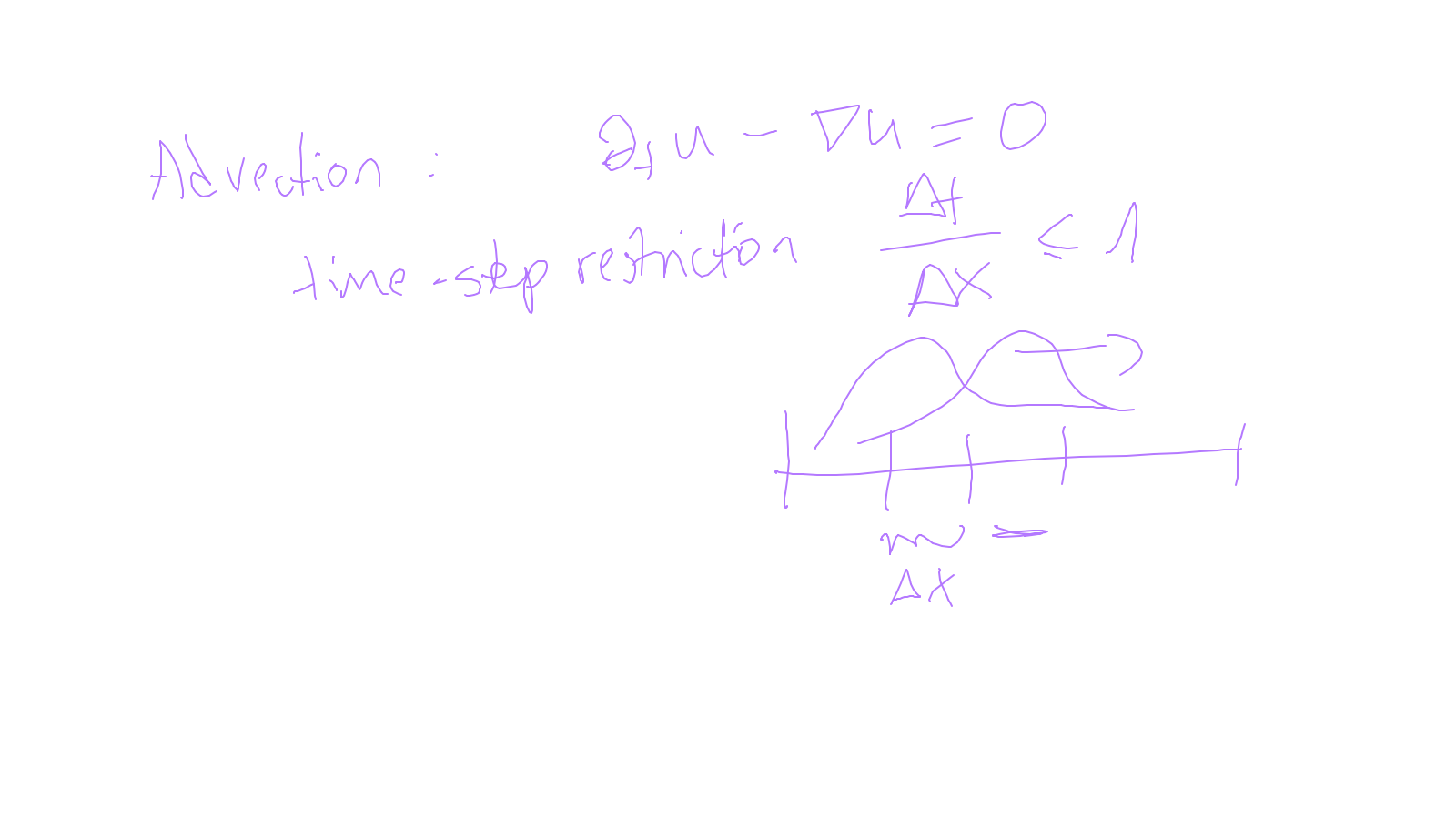
Lecture 10: space-time #
We will try to combine what we have learned in time-stepping and in spatial discretisations.
The video is now available at: video
The content of the whiteboard can be found below. It is also all contained in the ipython notebook itself.